题目内容
【题目】如图1所示为一张长为m，宽为n（m<n）的小长方形纸片，现将8张该纸片按如图2所示的方式无缝隙不重叠地放在长方形ABCD内，未被覆盖的部分（两个长方形）用阴影表示，设左上角与右下角的阴影部分面积差为S，当BC长度变化时，按照同样的方式放置，S却始终保持不变，则此时
=______．
【答案】3.
【解析】表示出左上角与右下角部分的面积，求出之差，根据差与BC无关即可求出m与n的关系式，由S却始终保持不变，得S与m，n之间的关系式，从而可求出结果.
如图，各点标记为：
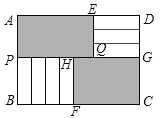
左上角阴影部分的长为AE，宽为AP=3m，右下角阴影部分的长为FC，宽为n，
∵AD=BC，即AE+ED=AE+n，BC=BF+FC=4m+FC，
∴AE+n=4m+FC，即AEFC=4mn，
∴阴影部分面积之差S=AEAPFCCG=3mAEnPC=3m(FC+4mn)nFC=(3mn)FC+12m23nm，
则3mn=0，即n=3m.
∵S却始终保持不变，
∴S
=(12m23nm)=
=3.
故答案为：3.
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
