题目内容
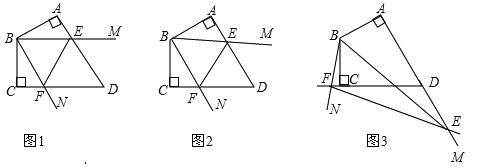
【题目】已知四边形ABCD中，AB=BC，∠ABC=120°，∠MBN=60°，∠MBN绕B点旋转，它的两边分别交AD，DC（或它们的延长线）于E，F．
当∠MBN绕B点旋转到AE=CF时（如图1），易证AE+CF=EF；
当∠MBN绕B点旋转到AE≠CF时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，线段AE，CF，EF又有怎样的数量关系？请写出你的猜想，不需证明．
【答案】证明见解析．
【解析】试题分析:对于图乙，将△BAE绕点B顺时针旋转120°到△BCE′，易知∠EBE′＝120°，F，C，E′三点共线，可证△BEF≌△BE′F，可得AE＋CF＝E′C＋CF＝E′F＝EF.对于图丙，类似可以得到AE－CF＝EF.
试题解析：
△BAE绕点B顺时针旋转120°到△BCE′，∴∠EBE′＝120°，∴F，C，E′三点共线，BE′= BF，∠ABC＝120°，∠MBN＝60°，∴∠ABE+∠CBF=120°，∴∠E′BC+∠CBF=120°，所以△BEF≌△BE′F，AE＋CF＝E′C＋CF＝E′F＝EF.
练习册系列答案
相关题目
