Question

【题目】已知点A（-8，0）及动点P（x，y），且2x-y＝-6.设三角形OPA的面积为S.

（1）当x＝-2时，点P坐标是____________；

（2）若点P在第二象限，且x为整数时，求y的值；

（3）是否存在第一象限的点P，使得S＝12.若存在，求点P的坐标；若不存在，

说明理由.

Answer 1

【答案】（1）（-2，2）；（2）当x＝-1时，y＝4；当x＝-2时，y＝2 ；（3）不存在.

【解析】（1）把x＝-2代入2x-y＝-6求出y的值，从而可得点P坐标；

（2）由点P在第二象限可得，即.然后根据x为整数，可求出y的值；

（3）若存在点P在第一象限，作PQ⊥x轴，垂足为Q，则根据三角形的面积公式可求出点P的坐标为（，3），与题意不符，从而不存在点P在第一象限.

⑴ P坐标是（-2，2） ；

⑵ ∵ 2x-y＝-6，

∴ y=2x+6，

∵ 点P在第二象限，

∴ 得 .

又∵ x是整数，

∴ x＝-1，-2，

当x＝-1时，y＝4，

当x＝-2时，y＝2 ；

⑶ 不存在.理由如下：

如图，∵点P在第一象限

作PQ⊥x轴，垂足为Q，则

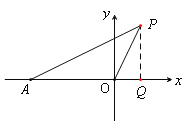
PQ＝2x+6

又 OA＝0-（-8）＝8、

S＝×OA×PQ＝12，即

×8×（2x+6）＝12，得

x＝，此时点P的坐标为（，3）

点P不在第一象限.