题目内容
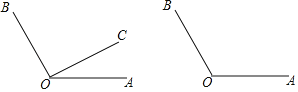
【题目】如图,∠AOB=120°,点C为平面内一点,作射线OC,射线OD平分∠BOC,射线OE平分∠AOD.
(1)若点C为∠AOB内部一点且∠AOC=30°,依题意补全图形,并求出∠EOC的度数;
(2)若点C为∠AOB内部一点,∠AOC=α(0<α<120°)直接用含α的代数式表示∠EOC的度数;
(3)若∠EOC=10°,请你直接写出所有符合条件的∠AOC度数(0<∠AOC<180°)
【答案】(1)补图详见解析,∠EOC=7.5°;(2)∠EOC=|![]() α﹣30°|;(3)∠AOC=
α﹣30°|;(3)∠AOC=![]() 或
或![]() .
.
【解析】
(1)首先求出∠COB的度数,然后根据角平分线的定义求得∠DOB=∠DOC=45°,那么∠DOA=75°,再根据角平分线的定义求得∠DOE,然后根据∠EOC=∠DOC-∠DOE求解;
(2)与(1)解法相同;
(3)根据(2)的结论解答即可.
解:(1)补全图形如图1所示,
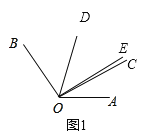
∵∠AOB=120°,∠AOC=30°,
∴∠COB=90°;
∵OD平分∠BOC,
∴∠DOB=∠DOC=45°;
∵∠AOB=120°,∠DOB=45°,
∴∠DOA=75°;
∵OE平分∠AOD,
∴∠DOE=∠AOE=37.5°;
∴∠EOC=∠DOC﹣∠DOE=45°﹣37.5°=7.5°;
(2)如图2所示,

∵∠AOB=120°,∠AOC=α,
∴∠COB=120°﹣α;
∵OD平分∠BOC,
∴∠DOB=∠DOC=60°﹣![]() α;
α;
∵∠AOB=120°,∠DOB=60°﹣![]() α,
α,
∴∠DOA=60°+![]() α;
α;
∵OE平分∠AOD,
∴∠DOE=∠AOE=30°+![]() α;
α;
∴∠EOC=|∠DOE﹣∠DOC|=|30°+![]() α﹣(60°﹣
α﹣(60°﹣![]() α)|=|
α)|=|![]() α﹣30°|.
α﹣30°|.
(3)如图所示,
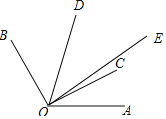
由(2)得,|![]() ∠AOC﹣30°|=10°,
∠AOC﹣30°|=10°,
解得∠AOC=![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
价格/类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
售价(元/盏) | 60 | 100 |
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?




