题目内容
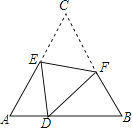
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB交AB于点E,且CD=AC,DF∥BC,分别与AB,AC交于点G,F.

(1)求证:GE=GF;
(2)填空:若BD=1,则DF的长是 .
【答案】(1)见解析 (2)1.5
【解析】
(1)根据已知条件易证明Rt△AEC≌Rt△DFC,得CE=CF,则DE=AF,从而进一步证明Rt△AFG≌Rt△DEG,就可得到GE=GF;
(2)根据直角三角形的性质可以得到CE=![]() AC,则CE=
AC,则CE=![]() CD,即AB是CE的垂直平分线,则BC=BD=1.再根据直角三角形的性质进一步求得AB、BE的长,则AE=AB-BE,结合(1)中的全等三角形,知DF=AE.
CD,即AB是CE的垂直平分线,则BC=BD=1.再根据直角三角形的性质进一步求得AB、BE的长,则AE=AB-BE,结合(1)中的全等三角形,知DF=AE.
解:(1)证明:∵DF∥BC,∠ACB=90°,
∴∠CFD=90°,
∵CD⊥AB,
∴∠AEC=90°,
在△AEC和△DFC中,
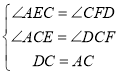
∴△AEC≌△DFC(AAS),
∴CE=CF,
∴AF=DE,
在△AFG和△DEG中,
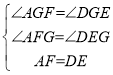 ,
,
∴△AFG≌△DEG(AAS),
∴GE=GF;
(2)∵CD⊥AB,∠A=30°,
∴CE=![]() AC=
AC=![]() CD,
CD,
∴CE=ED.
∴BC=BD=1.
又∵∠ECB+∠ACE=90°,∠A+∠ACE=90°,
∴∠ECB=∠A=30°,∠CEB=90°,
∴BE=![]() BC=
BC=![]() BD=
BD=![]() ,
,
在直角三角形ABC中,∠A=30°,
则AB=2BC=2.
则AE=AB-BE=![]() ,
,
∵△AEC≌△DFC,
∴DF=AE=![]() =1.5,
=1.5,
故答案为:1.5

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目