题目内容
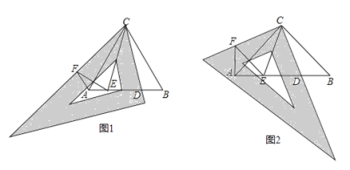
【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别是BE,CD的中点,
(1)求证:△AMN是等边三角形.
(2)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由.
【答案】
(1)证明:∵△ABC和△ADE是等边三角形,
∴AB=AC,AE=AD, ∠BAC=∠EAD=60°,
∴AB-AE=AC-AD,即BE=CD,
∴M,N分别是BE,CD的中点,
∴EM= ![]() BE,DN=
BE,DN= ![]() CD, ∴EN=DN,
CD, ∴EN=DN,
∴EM+AE=DN+AD,即AN=AM,
∵∠BAC=60°,
∴△AMN是等边三角形
(2)解:CD=BE.理由如下:
∵△ABC和△ADE为等边三角形,∴AB=AC,AE=AD,∠BAC=∠EAD=60°.
∵∠BAE=∠BAC∠EAC=60°∠EAC,∠DAC=∠DAE∠EAC=60°∠EAC,∠BAE=∠DAC,∴△ABE≌△ACD,∴CD=BE.
【解析】(1) 要证△AMN是等边三角形,根据已知条件可知只需证明AN=AM,根据△ABC和△ADE是等边三角形,得出BE=CD,再根据中点定义得出EN=DN, 就可证得AN=AM,根据一个角等于60°的等腰三角形是等边三角形,即可得证。
(2)CD=BE仍然成立,根据已知条件证明△ABE≌△ACD即可。

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目