题目内容
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-1,3),B(-2,1),C(-3,1).
(1)①画出△ABC关于y轴对称的△A1B1C1 , 并写出A1点的坐标及sin∠B1C1A1的值;
②以原点O为位似中心,位似比为1:2,在y轴的左侧,画出将△ABC放大后的△A2B2C2 , 并写出A2点的坐标;
(2)若点D为线段BC的中点,直接写出经过(2)的变化后点D的对应点D2的坐标.
【答案】
(1)解:如图,△A1B1C1 , △A2B2C2即为所求,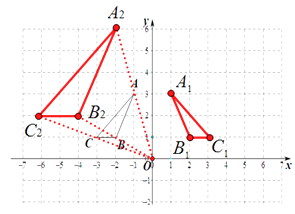
①∴A1(1,3),sin∠B1 C1A1=sin45°= ![]()
②∴A2(2,6)
(2)解:∵点D在线段BC的中点上,
∴D(-2.5,1),
∵位似比为1:2,
∴D2(-5,2)
【解析】利用关于y轴对称点的性质得出对应点坐标进而求出即可;利用位似图形的性质得出对应点位置即可得出答案;利用位似比得出对应点坐标的变化规律进而得出答案.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目