题目内容
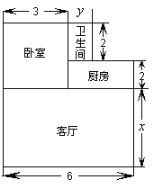
【题目】五一假期过后,小明到校后发现忘记带数学课本,一看手表,离上课还有20分钟,他立刻步行返回家中取书,同时,他的父亲也发现小明忘记带数学课本,带上课本立刻以小明步行速度的2倍骑车赶往学校.父子在途中相遇,小明拿到课本后马上按原速步行返回学校,到校后发现迟到了4分钟.如图是父子俩离学校的路程s(米)与所用时间t(分)之间的函数关系,请结合图像,回答下列问题:
(1)两人相遇处离学校的距离是多少米?
(2)试求小明的父亲在赶往学校的过程中,路程s与时间t之间的函数表达式;
(3)假如小明父子相遇拿到课本后,改由他的父亲骑车搭他到学校,他会迟到吗?如果会,迟到几分钟;如果不会,能提前几分钟到校?
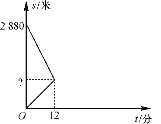
【答案】(1)两人相遇处离学校的距离是960米;(2) s=-160t+2880;(3)如果由他的父亲骑车搭他到学校,他不会迟到,且能提前2分钟到校.
【解析】
(1) 设小明步行速度为x米/分,则小明父亲骑车速度为2x米/分,根据两人12分钟的路程为2880米列方程,从而求得小明的速度,从而得到问题的解;
(2) 设小明的父亲在赶往学校的过程中,路程s与时间t之间的函数关系式为s=kt+b,再将(0,2 880)和(12,960)分别代入得到关于k、t的方程组,解方程组即可得到问题的解;
(3) 令s=0,得出t的值,再与20进行比较即可得出问题的解.
(1)在图像中可以看出,从出发到父子相遇花费了12分钟.
设小明步行速度为x米/分,则小明父亲骑车速度为2x米/分,根据题意,得
12x+12×2x=2 880.解得x=80.
∴两人相遇处离学校的距离是80×12=960(米).
(2)设小明的父亲在赶往学校的过程中,路程s与时间t之间的函数关系式为s=kt+b.
把(0,2 880)和(12,960)分别代入,得
![]() 解得
解得![]() ,
,
∴s=-160t+2 880.
(3)在s=-160t+2880中,令s=0,得0=-160t+2 880.
解得t=18.
∴20-18=2(分钟).
∴如果由他的父亲骑车搭他到学校,他不会迟到,且能提前2分钟到校.

 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】一分钟投篮测试规定,得6分以上为合格,得9分以上为优秀,甲、乙两组同学的一次测试成绩如下:
成绩(分) | 4 | 5 | 6 | 7 | 8 | 9 |
甲组(人) | 1 | 2 | 5 | 2 | 1 | 4 |
乙组(人) | 1 | 1 | 4 | 5 | 2 | 2 |
(1)请你根据上述统计数据,把下面的图和表补充完整; 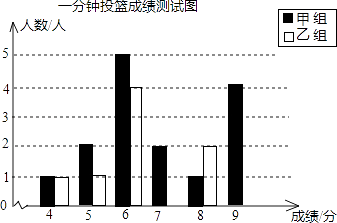
一分钟投篮成绩统计分析表:
统计量 | 平均分 | 方差 | 中位数 | 合格率 | 优秀率 |
甲组 | 2.56 | 6 | 80.0% | 26.7% | |
乙组 | 6.8 | 1.76 | 86.7% | 13.3% |
(2)下面是小明和小聪的一段对话,请你根据(1)中的表,写出两条支持小聪的观点的理由.