Question

【题目】如图，直线AB和直线CD相交于O点，OE⊥OD，OF平分∠AOE，∠BOD＝26°

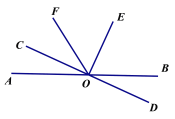
(1)写出∠COB的邻补角。

(2)求∠COF的度数

Answer 1

【答案】（1）∠AOC 和 ∠BOD；（2） ∠COF=32°.

【解析】

（1）根据邻补角的定义（两个角有一条公共边，它们的另一条边互为反向延长线，具有这种关系的两个角，叫做邻补角）进行判断即可；

（2）根据垂直和对顶角的定义可得∠COE=90°、∠AOC=26°，然后根据角平分线的定义求出∠COF的度数即可.

解：（1）∠COB的邻补角为∠AOC 和 ∠BOD；

（2）解：∵OE⊥CD，
∴∠COE =90°，
∵∠BOD＝26°，

∴∠AOC=26°，

设∠COF为x，

∵∠AOF=∠EOF，

∴∠EOF=26°+x，

又∵∠COE =90°，

∴x+26°+x=90°

x=32°.

故∠COF=32°