题目内容
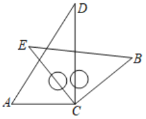
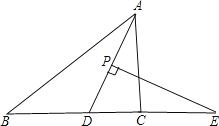
【题目】如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.
(1)若∠B=30°,∠ACB=80°,求∠E的度数;
(2)当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.
【答案】(1)∠E=25°;(2)∠E=![]() (∠ACB﹣∠B).
(∠ACB﹣∠B).
【解析】
(1)首先根据三角形的内角和定理求得∠BAC的度数,再根据角平分线的定义求得∠DAC的度数,从而根据三角形的内角和定理即可求出∠ADC的度数,进一步求得∠E的度数;
(2)根据第(1)小题的思路即可推导这些角之间的关系.
解:(1)∵∠B=30°,∠ACB=80°,
∴∠BAC=70°,
∵AD平分∠BAC,
∴∠DAC=35°,
∴∠ADC=65°,
∴∠E=25°;
(2)∠E=![]() (∠ACB﹣∠B).
(∠ACB﹣∠B).
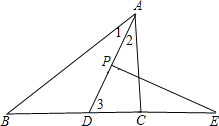
设∠B=n°,∠ACB=m°,
∵AD平分∠BAC,
∴∠1=∠2=![]() ∠BAC,
∠BAC,
∵∠B+∠ACB+∠BAC=180°,
∵∠B=n°,∠ACB=m°,
∴∠CAB=(180-n-m)°,
∴∠BAD=![]() (180-n-m)°,
(180-n-m)°,
∴∠3=∠B+∠1=n°+![]() (180-n-m)°=90°+
(180-n-m)°=90°+![]() n°-
n°-![]() m°,
m°,
∵PE⊥AD,
∴∠DPE=90°,
∴∠E=90°-(90°+![]() n°-
n°-![]() m°)=
m°)=![]() (m-n)°=
(m-n)°=![]() (∠ACB-∠B).
(∠ACB-∠B).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
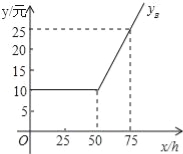
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?