Question

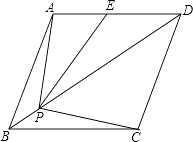
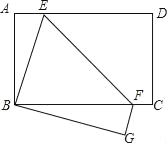
【题目】如图，直线AB∥CD，直线l与直线AB，CD相交于点E，F，点P是射线EA上的一个动点（不包括端点E），将△EPF沿PF折叠，使顶点E落在点Q处．

⑴若∠PEF＝48°,点Q恰好落在其中的一条平行线上,则∠EFP的度数为 ．

⑵若∠PEF＝75°，∠CFQ＝∠PFC，求∠EFP的度数．

Answer 1

【答案】⑴ ∠EFP=42°或66°

⑵∠EFP的度数为35°或63°.

【解析】

试题 当点落在上，根据三角形的内角和即可得到结论；当点落在上，由折叠的性质得到垂直平分，得到，根据平行线的性质即可得到结论；
①如图，当点在平行线，之间时，设，由折叠可得根据平行线的性质即可得到结论；②如图，当点在的下方时，设 由得，.根据平行线的性质即可得到结论．

试题解析： 或

ⅰ如图1，当点在平行线，之间时：

设的度数为，由折叠可得：

,

解得：

即：

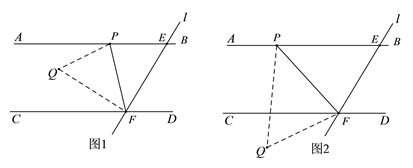
ⅱ如图2，当点在的下方时,

设

由得：

由折叠得

解得：

综上：的度数为或