ЬтФПФкШн
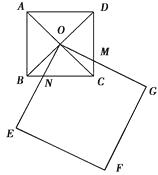
ЁОЬтФПЁПвбжЊЃЌдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌЁЯABCЃН45ЁуЃЌABЃНACЃЌЕуDЮЊжБЯпBCЩЯвЛЖЏЕу(ЕуDВЛгыBЃЌCжиКЯ)ЃЌвдADЮЊБпзїе§ЗНаЮADEFЃЌСЌНгCFЃЎ
(1)ЙлВьВТЯы
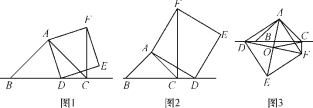
ШчЭМ1ЃЌЕБЕуDдкЯпЖЮBCЩЯЪБПЩвджЄУїЁїABDЁеЁїACFЃЌдђ
ЂйBCгыCFЕФЮЛжУЙиЯЕЮЊЃК ЃЛ
ЂкBCЃЌDCЃЌCFжЎМфЕФЪ§СПЙиЯЕЮЊЃК ЃЛ
(2)РрБШЬНОП
ШчЭМ2ЃЌЕБЕуDдкЯпЖЮBCЕФбгГЄЯпЩЯЪБЃЌЦфЫћЬѕМўВЛБфЃЌ(1)жаЂйЃЌЂкНсТлЪЧЗёШдШЛГЩСЂЃПШєГЩСЂЃЌЧыИјгшжЄУїЃЛШєВЛГЩСЂЃЌЧыФуаДГіе§ШЗНсТлдйИјгшжЄУїЃЛ
(3)ЭиеЙбгЩь
ШчЭМ3ЃЌЕБЕуDдкЯпЖЮBCЕФЗДЯђбгГЄЯпЩЯЪБЃЌЧвЕуAЃЌFЗжБ№дкжБЯпBCЕФСНВрЃЌЦфЫћЬѕМўВЛБфЃЎ
ЂйBCЃЌDCЃЌCFжЎМфЕФЪ§СПЙиЯЕЮЊЃК
ЂкШєе§ЗНаЮADEFЕФБпГЄЮЊ2ЃЌЖдНЧЯпAEЃЌDFЯрНЛгкЕуOЃЌСЌНгOCЃЌдђOCЕФГЄЖШЮЊ ЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйBCЁЭCFЃЛЂкBCЃНDCЃЋCFЃЛЃЈ2ЃЉЂйГЩСЂЃЌЂкВЛГЩСЂЃЌНсТлЂкгІИФЮЊBCЃНCFЃDCЃЌРэгЩЯъМћНтЮіЃЛЃЈ3ЃЉЂйBCЃНDCЃCFЃЛЂк![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЂйИљОнSASжЄУїЁїABDЁеЁїACFЃЌПЩЕУЁЯABCЃНЁЯACFЃН45ЁуЃЌдђЁЯBCFЃНЁЯACBЃЋЁЯACFЃН90ЁуЃЌЫљвдBCЁЭCFЃЛ
ЂкгЩЁїABDЁеЁїACFЕФаджЪКЭЯпЖЮЕФКЭПЩЕУНсТлЃЛ
ЃЈ2ЃЉЂйГЩСЂЃЌжЄУїЁЯBACЃЋЁЯCADЃНЁЯDAFЃЋЁЯCADЃЌМДЁЯBADЃНЁЯCAFЃЌЭЌРэжЄУїЁїABDЁеЁїACFЃЌПЩЕУBCЁЭCFЃЌ
ЂкВЛГЩСЂЃЌгЩBDЃНBCЃЋCDЃЌBDЃНCFЃЌПЩЕУаТЕФНсТлЃКBCЃНCFDCЃЛ
ЃЈ3ЃЉЂйИљОнЭМ3жЊЃКDCзюГЄЃЌЭЌРэЃКЁїDABЁеЁїFACЃЌдђBDЃНCFЃЌПЩЕУBCЃНDCCFЃЛ
ЂкЯШИљОне§ЗНаЮЕФБпГЄЧѓЖдНЧЯпDFЕФГЄЃЌжЄУїЁЯDCFЃН90ЁуЃЌИљОнжБНЧШ§НЧаЮаББпжаЯпЕФаджЪПЩЕУOCЕФГЄЃЎ
ЃЈ1ЃЉЂйBCЁЭCFЃЌРэгЩЪЧЃК
ШчЭМ1ЃЌЁпЫФБпаЮADEFЪЧе§ЗНаЮЃЌ
ЁрЁЯDAFЃН90ЁуЃЌADЃНAFЃЌ
ЁпЁЯBACЃН90ЁуЃЌ
ЁрЁЯBADЃЋЁЯDACЃНЁЯDACЃЋЁЯCAFЃЌ
ЁрЁЯBADЃНЁЯCAFЃЌ
дкЁїBADКЭЁїCAFжаЃЌ
Ёп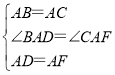 ЃЌ
ЃЌ
ЁрЁїBADЁеЁїCAFЃЈSASЃЉЃЌ
ЁрЁЯABCЃНЁЯACFЃН45ЁуЃЌ
ЁпЁЯACBЃН45ЁуЃЌ
ЁрЁЯBCFЃНЁЯACBЃЋЁЯACFЃН90ЁуЃЌ
ЁрBCЁЭCFЃЛ
ЂкBCЃНDCЃЋCFЃЌ
РэгЩЪЧЃКгЩЂйжЊЃКЁїABDЁеЁїACFЃЌ
ЁрBDЃНCFЃЌ
ЁрBCЃНBDЃЋCDЃНCFЃЋCDЃЛ
ЙЪД№АИЮЊЃКЂйBCЁЭCFЃЌЂкBCЃНCFЃЋCDЃЛ
ЃЈ2ЃЉЂйГЩСЂЃЌЂкВЛГЩСЂЃЌНсТлЂкгІИФЮЊBCЃНCFDCЃЛ
жЄУїЃКШчЭМ2ЃЌдке§ЗНаЮADEFжаЃЌ
ADЃНAFЃЌЁЯDAFЃН90ЁуЃЌ
ЁпЁЯBACЃН90ЁуЃЌ
ЁрЁЯBACЃЋЁЯCADЃНЁЯDAFЃЋЁЯCADЃЌМДЁЯBADЃНЁЯCAFЃЌ
ЁпЁЯABCЃН45ЁуЃЌ
ЁрЁЯACBЃН180ЁуЁЯBACЁЯABCЃН45ЁуЃЌ
ЁрЁЯABCЃНЁЯACBЃЌ
ЁрABЃНACЃЌ
дкЁїABDгыЁїACFжаЃЌ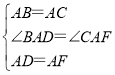 ЃЌ
ЃЌ
ЁрЁїABDЁеЁїACFЃЌ
ЁрЁЯACFЃНЁЯABDЃН45ЁуЃЌBDЃНCFЃЌ
ЁпЁЯACBЃН45ЁуЃЌ
ЁрЁЯBCFЃНЁЯACBЃЋЁЯACFЃН90ЁуЃЌ
ЁрBCЁЭCFЃЛ
ЁпBDЃНBCЃЋCDЃЌBDЃНCFЃЌ
ЁрBCЃНCFDCЃЛ
ЃЈ3ЃЉЂйBCЃНDCCFЃЌ
РэгЩЪЧЃКШчЭМ3ЃЌЭЌРэЕУЃКЁЯDABЃНЁЯFACЃЌ
взжЄЕУЃКЁїDABЁеЁїFACЃЌ
ЁрBDЃНCFЃЌ
ЁрDCЃНBDЃЋBCЃНCFЃЋBCЃЌ
ЁрBCЃНDCCFЃЛ
Ђке§ЗНаЮADEFжаЃЌБпГЄEFЃН2
ЁрDFЃН2![]()
ЁпЁЯABCЃН45Ёу
ЁрЁЯABDЃН135Ёу
ЁпЁїDABЁеЁїFAC
ЁрЁЯACFЃНЁЯABDЃН135Ёу
ЁпЁЯACBЃН45Ёу
ЁрЁЯDCFЃН90Ёу
ЁпЫФБпаЮADEFЪЧе§ЗНаЮ
ЁрODЃНOF
ЁрOCЃН![]() DFЃН
DFЃН![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃКЂйBCЃНDCCFЃЌЂк![]() ЃЎ
ЃЎ