题目内容
【题目】如图四边形ABCD和四边形OEFG都是正方形,点O是正方形ABCD两对角线的交点,已知AB=2,EF=3,正方形OEFG绕点O转动,OE交BC上一点N,OG交CD上一点M.求四边形OMCN的面积.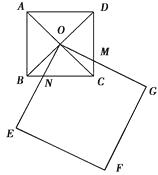
【答案】解:∵四边形ABCD是正方形,对角线AC、BD相交
于点O,
∴OB=OC,∠4=∠5=45°,∠BOC=90°,
即∠1+∠2=90°.
又∵四边形OEFG是正方形,
∴∠EOG=90°,
即∠2+∠3=90°,
∴∠1=∠3.
在△BON和△COM中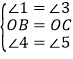
∴△BON≌△COM(ASA)
∴S四边形OMCN=S△ONC+S△OCM=S△ONC+S△BON
=S△BOC=![]() S正方形ABCD=
S正方形ABCD=![]() ×22=1.
×22=1.
即四边形OMCN的面积为1.
【解析】考查全等三角形的判定与性质。
【考点精析】本题主要考查了正方形的性质和旋转的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目