题目内容
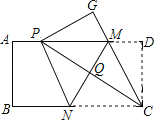
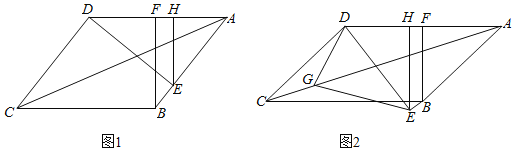
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() BF的长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为12,∠C=60°,则四边形ABEF的面积是( )
BF的长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为12,∠C=60°,则四边形ABEF的面积是( )

A.9![]() B.12C.
B.12C.![]() D.6
D.6
【答案】C
【解析】
根据题意可知AE是∠BAF的角平分线,根据平分线性质和AF=AB,可证明四边形ABEF是菱形,菱形的对角线相互垂直平分,再由∠C=![]() ,可得△ABF为正三角形,再由
,可得△ABF为正三角形,再由![]() 所对直角边是斜边一半,可以算出AG的长,四边形ABEF面积即可算出.
所对直角边是斜边一半,可以算出AG的长,四边形ABEF面积即可算出.
由作法得AE平分∠BAD,AB=AF,
则∠1=∠2,
∵四边形ABCD为平行四边形,
∴BE∥AF,∠BAF=∠C=60°,
∴∠2=∠BEA,
∴∠1=∠BEA=30°,
∴BA=BE,
∴AF=BE,
∴四边形AFEB为平行四边形,△ABF是等边三角形,
而AB=AF,
∴四边形ABEF是菱形;
∴BF⊥AE,AG=EG,
∵四边形ABEF的周长为12,
∴AF=BF=AB=3,
在Rt△ABG中,∠1=30°,
∴BG=![]() AB=1.5,AG=
AB=1.5,AG=![]() BG=
BG=![]() ,
,
∴AE=2AG=3![]() ,
,
∴菱形ABEF的面积=![]() BF×AE=
BF×AE=![]() ×3×3
×3×3![]() =
=![]() ;
;
故选:C.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
【题目】如图,Rt△ACB中,∠ACB=90°,AC=2BC=4,点P为AB边中点,点E为AC边上不与端点重合的一动点,将△ADP沿着直线PD折叠得△PDE,若DE⊥AB,则AD的长度为_____ .