题目内容
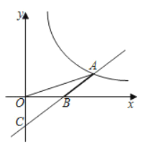
【题目】如图,直线y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
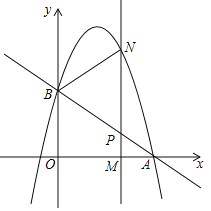
(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为线段OA上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
①试用含m的代数式表示线段PN的长;
②求线段PN的最大值.
【答案】(1)B(0,2),y=﹣![]() x2+
x2+![]() x+2;(2)①PN=﹣
x+2;(2)①PN=﹣![]() (0≤m≤3);②m=
(0≤m≤3);②m=![]() 时,线段PN有最大值为3.
时,线段PN有最大值为3.
【解析】
(1)把A点坐标代入直线解析式可求得c,则可求得B点坐标,由A、B的坐标,利用待定系数法可求得抛物线解析式;
(2)①M(m,0),则P(m,![]() ),N(m,﹣
),N(m,﹣![]() ),即可求出PN的长;
),即可求出PN的长;
②根据二次函数的性质可得线段PN的最大值.
解:(1)∵y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,
x+c与x轴交于点A(3,0),与y轴交于点B,
∴0=﹣2+c,解得c=2,
∴B(0,2),
∵抛物线y=﹣![]() x2+bx+c经过点A,B,
x2+bx+c经过点A,B,
∴![]() ,解得
,解得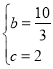 ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)①M(m,0),则P(m,![]() ),N(m,﹣
),N(m,﹣![]() ),
),
∴PN=![]() =﹣
=﹣![]() (0≤m≤3);
(0≤m≤3);
②∵PN=﹣![]() =
=![]() ,
,
∴m=![]() 时,线段PN有最大值为3.
时,线段PN有最大值为3.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?