题目内容
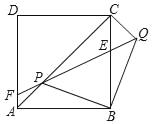
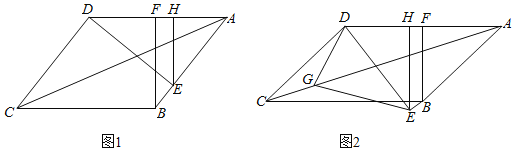
【题目】如图,在平行四边形ABCD中,AC为对角线,过点D作DE⊥DC交直线AB于点E,过点E作EH⊥AD于点H,过点B作BF⊥AD于点F.
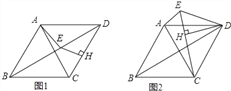
(1)如图1,若∠BAD=60°,AF=3,AH=2,求AC的长;
(2)如图2,若BF=DH,在AC上取一点G,连接DG、GE,若∠DGE=75°,∠CDG=45°﹣∠CAB,求证:DG=![]() CG.
CG.
【答案】(1)AC=2![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)注意到∠CBA=120°,于是作AM⊥CB于M,先求出CM与AM的长度,再由勾股定理算出AC长度.
(2)由已知条件可以直接判断出△DEH≌△BAF,然后可推出CD=DE,于是连接CE,作EN⊥AC于N,连接DN,可以证明△DGN是等腰直角三角形以及△CDG≌△EDN,注意到∠EGD=75°,从而∠EGN=30°,所证结论就自然成立了.
(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,CD=AB,CD∥AB,
∵BF⊥AD于F,
∴∠AFB=90°,
∵∠BAD=60°,
∴AB=2AF=6,BF=![]() AF=3
AF=3![]() ,
,
∵EH⊥AD于H,
∴AE=2AH=4,EH=![]() AH=2
AH=2![]() ,
,
∵DE⊥DC交AB于E,
∴∠DEA=90°,
∴AD=2AE=8,
∴CB=AD=8,
如图1,作AM⊥CB于M,则∠ABM=∠BAD=60°,
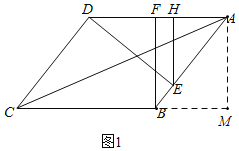
∴BM=(1/2)AB=3,AM=![]() BM=3
BM=3![]() ,
,
∴CM=CB+BM=11,
在Rt△ACM中:AC=![]() =
=![]() =2
=2![]() .
.
(2)如图2,作EN⊥AC于N,连接DN、CE,则∠CNE=90°.
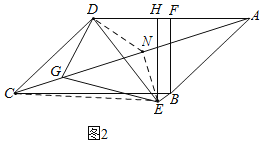
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,CD=AB,CD∥AB,
∵DE⊥DC交AB于E,
∴∠CDE=∠DEA=90°,
∵EH⊥AD于H,
∴∠DHD=∠EHA=90°,
∵BF⊥AD于F,
∴∠DFB=∠AFB=90°,
∴∠DHE=∠BFA,
∵∠DEH+∠HEA=∠HEA+∠BAF=90°,
∴∠DEH=∠BAF,
∵DH=BF,
∴△DEH≌△BAF(AAS),
∴DE=BA=CD,
∴△CDE是等腰直角三角形,∠DCE=∠DEC=45°,
∵∠CDE=∠CNE=90°,
∴C、D、N、E四点共圆,
∴∠DNC=∠DEC=45°,
∵∠CDG=45°﹣∠CAB,
∴∠CDG+∠CAB=45°,
∵CD∥AB,
∴∠CAB=∠DCG,
∴∠DGN=∠DCG+∠CDG=45°=∠DNC,
∴△DGN是等腰直角三角形,∠GDN=90°,DG=DN,
∵∠CDG+∠GDE=∠GDE+∠EDN=90°,
∴∠CDG=∠EDN,
∴△CDG≌△EDN(SAS),
∴EN=CG,
∵∠CGD=75°,
∴∠CGN=∠CGD﹣∠DGN=30°,
∴GN=![]() EN=
EN=![]() CG,
CG,
∴DG=![]() GN=
GN=![]() CG
CG