��Ŀ����
����Ŀ����ѧ��ȤС��������Ӷ����Ŵ���C��D֮��ľ��룮��ͼ��ʾ���ںӰ�A���ô���Cλ�����������ϣ�����Dλ�ڱ�ƫ��42�������ϣ����غӰ���ǰ��100����B������ô���Dλ�ڱ�ƫ��31�������ϣ������Ŵ���C��D֮��ľ��룮�������ȷ��1�ף��ο����ݣ�sin31���0.52��cos31���0.86��tan31���0.60��sin42���0.67��coo42���0.74��tan42���0.90����
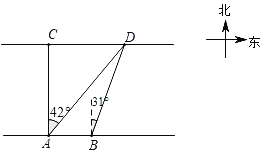
���𰸡����Ŵ���C��D֮��ľ���ԼΪ300�ף�
��������
����ͼ������D��DE��AB������Ϊ��E����CD=x�ף���Rt��ACD�У������DE�ij���Ȼ����Rt��BED�У����BE�ij����Ӷ��ó�x��ֵ��
��ͼ������D��DE��AB������Ϊ��E��
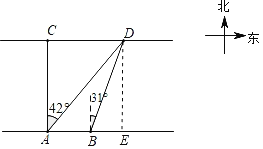
������֪����ACD����CAE����AED��90����
���ı���ACDE�Ǿ��Σ�
��AC��ED��CD��AE��
��CD��x�ף���BE��(x��100)�ף�
��Rt��ACD��tan��ADE��![]() ��
��
��DE��![]() ��
��![]() x��
x��
��Rt��BED��tan��BDE��![]() ��
��
��BE��![]() x��
x��![]() ��
��![]() x��
x��
������ã�x��![]() x��100��
x��100��
��ã�x��300��
�����Ŵ���C��D֮��ľ���ԼΪ300�ף�

��ϰ��ϵ�д�
�����Ŀ