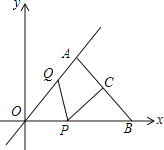
题目内容
【题目】已知:如图点![]() 在正比例函数图象上,点
在正比例函数图象上,点![]() 坐标为
坐标为![]() ,连接
,连接![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上以每秒2个单位的速度由点
上以每秒2个单位的速度由点![]() 向点
向点![]() 运动,点
运动,点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 运动,
运动,![]() 两点同时运动,同时停止,运动时间为
两点同时运动,同时停止,运动时间为![]() 秒.
秒.
(1)正比例函数的关系式为 ;
(2)当![]() 秒,且
秒,且![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)连接![]() ,在点
,在点![]() 运动过程中,
运动过程中,![]() 与
与![]() 是否全等?如果全等,请求出点
是否全等?如果全等,请求出点![]() 的运动速度;如果不全等,请说明理由.
的运动速度;如果不全等,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当点
;(3)当点![]() 的运动速度是每秒
的运动速度是每秒![]() 个单位或每秒
个单位或每秒![]() 个单位时,
个单位时,![]() 与
与![]() 全等.
全等.
【解析】
(1)设正比例函数的解析式为y=kx,然后将点A的坐标代入求解即可;
(2)过点Q作QH⊥x轴于点H,由t=1,可知BP=2,从而可求得OP=10,然后根据三角形的面积公式可求出QH的长,又点Q在正比例函数图象上,从而可得出点Q的坐标;
(3)由OA=AB=10得到∠QOP=∠CBP,由△OPQ与△BPC全等可知:OP=BC=5,OQ=BP或OQ=BC=5,OP=PB,再分别求出AQ的长,从而可求得点Q的运动速度.
解:(1)设正比例函数的解析式为y=kx,
把A(6,8)代入得:8=6k.
解得:k=![]() .
.
故答案为:y=![]() x;
x;
(2)当t=1时,BP=2,OP=10.
如图,过点Q作QH⊥x轴于点H,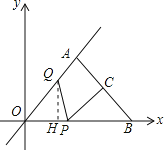
∵S△OPQ=![]() OPQH=6,∴QH=
OPQH=6,∴QH=![]() .
.
把Q(x,![]() )代入y=
)代入y=![]() x中,得x=
x中,得x=![]() ,
,
∴点Q的坐标为(![]() ,
,![]() );
);
(3)∵AO=AB=10,点C是线段AB的中点,
∴BC=5,∠QOP=∠CBP.
若△OPQ与△BPC全等,
则有OP=BC=5,OQ=BP或OQ=BC=5,OP=PB.
设Q点的运动速度为v个单位/秒,
①OP=BC=5,OQ=BP时,
∵OP=5,∴12-2t=5.解得t=![]() .
.
∴OQ=BP=2×![]() =7.
=7.
∴AQ=10-7=3.
∴![]() v=3,解得v=
v=3,解得v=![]() .
.
∴点Q运动的速度为![]() 个单位/秒.
个单位/秒.
②当OQ=BC=5,OP=PB=6时,
由OP=PB=![]() OB=6可知:2t=6,
OB=6可知:2t=6,
解得:t=3.
∵OQ=5,∴AQ=OA-OQ=10-5=5.
∴3v=5,解得v=![]() .
.
∴点Q运动的速度为![]() 个单位/秒.
个单位/秒.
综上所述:当点Q的运动速度是每秒![]() 个单位或每秒
个单位或每秒![]() 个单位时,△OPQ与△BPC全等.
个单位时,△OPQ与△BPC全等.