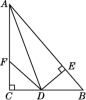题目内容
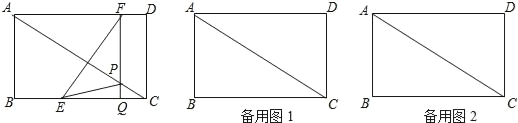
【题目】如图，在△ABC 中，AD⊥BC 于点 D，点 E 为BD边上一点，过点 E 作 EG∥AD，分别交 AB 和 CA 的延长线于点 F，G，∠AFG=∠G．
（1）证明：△ABD≌△ACD
（2）若∠B=40°，直接写出∠FAG= °
【答案】（1）详见解析；（2）80
【解析】
（1）由已知条件可直接得到AD为公共边，∠ADB＝∠ADC＝90°，据两直线平行间接可得到∠CAD＝∠BAD，即可判定△ABD≌△ACD（ASA）；
（2）利用（1）中结论易求得∠C度数，根据三角形外角的性质即可得
的度数．
解：（1）∵
，
∴
∵
，
∴
，
．
∵
，
∴
．
在
和
中，
∴≌（
）
（2）解：由（1）≌可得：
，
∵∠B＝40°，
∴∠C＝40°，
∴
，
故答案为：
．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】为了从甲、乙两人中选拔一人参加射击比赛，现对他们的射击成绩进行了测试，5次打靶命中的环数如下：
甲：8，7，10，7，8； 乙：9，5，10，9，7；
(1)将下表填写完整：
平均数 | 极差 | 方差 | |
甲 | 3 | 1.2 | |
乙 | 8 | 3.2 |
（2）根据以上信息，若你是教练，选择谁参加射击比赛，理由是什么？
（3）若乙再射击一次，命中8环，则乙这六次射击成绩的方差会 ．（填变大或变小或不变
