题目内容
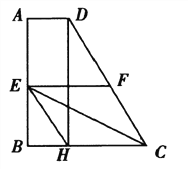
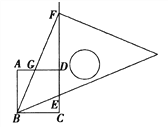
【题目】如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在点B处,直角顶点F在CD的延长线上,BF与AD交于点G,斜边与CD交于点E![]() ,若CE=1,则DG的长为( )
,若CE=1,则DG的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
【答案】B
【解析】试题解析:如图将△BCE绕点B逆时针旋转90°得到△BAM.BF与AD交于点G.
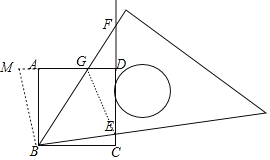
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=3,∠ABC=90°,
∵∠GBE=45°,
∴∠CBE+∠GBA=∠ABM+∠GBA=45°=∠GBM,
∵BG=BG,∠GBM=∠GBE,BE=BM,
∴△BGM≌△BGE,
∴EG=GM=AM+AG=AG+CE,设AG=x,则DG=3-x,GE=1+x,
在Rt△DGE中,∵GE2=DG2+DE2,
∴(3-x)2+22=(x+1)2,
∴x=![]() ,
,
∴DG=![]() .
.
故选B.

练习册系列答案
相关题目