Question

【题目】如图，在四边形ABCD中，AD∥BC，AB⊥BC，AD=2，BC=6，CD=8，E，F分别是边ABCD的中点, DH⊥BC于点H，连接EH，EC，EF，现有下列结论:①∠CDH=30°；②EF=4;③四边形EFCH是菱形;④S△EFC=3S△BEH.你认为结论正确的有___________.(填序号)

Answer 1

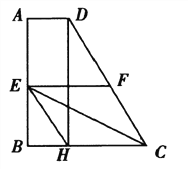
【答案】①②③

【解析】试题解析：①∵AD∥BC，AB⊥BC，DH⊥BC，

∴四边形ABHD是矩形，

∴BH=AD=2，AB=DH，

∴CH=BC-BH=6-2=4，

∵CD=8，

∴CH=CD，

∴∠CDH=30°；①正确；

②∵E，F分别是边AB、CD的中点，

∴CF=CD=4，EF∥BC，EF=（AD+BC）=4，②正确；

③∵EF∥BC，EF=CH=4，

∴四边形EFCH是平行四边形，

又∵EF=CF=4，

∴四边形EFCH是菱形；③正确；

④∵EF=4，BH=2，

∴S△EFC=2S△BEH．④错误；

故选：①②③．