题目内容
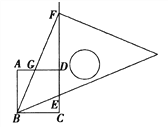
【题目】在Rt△ABC中，∠ACB=90°，∠A=30°，点D是AB的中点，DE⊥BC，垂足为点E，连接CD．
（1）如图1，求DE与BC的数量关系；
（2）如图2，若P是线段CB上一动点（点P不与点B、C重合），连接DP，将线段DP绕点D逆时针旋转60°，得到线段DF，∠PDF=60°连接BF，请猜想DE、BF、BP三者之间的数量关系，并证明你的结论；
【答案】（1）DE=
BC．
（2）BF+BP=
DE．理由见解析
【解析】试题分析：（1）由∠ACB=90°，∠A=30°得到∠B=60°，根据直角三角形斜边上中线性质得到DB=DC，则可判断△DCB为等边三角形，由于DE⊥BC，DE=
BC；
（2）根据旋转的性质得到∠PDF=60°，DP=DF，易得∠CDP=∠BDF，则根据“SAS”可判断△DCP≌△DBF，则CP=BF，利用CP=BC﹣BP，DE=
BC可得到BF+BP=
DE．
试题解析：解：（1）∵∠ACB=90°，∠A=30°，∴∠B=60°．∵点D是AB的中点，∴DB=DC，∴△DCB为等边三角形．∵DE⊥BC，∴DE=
BC．故答案为： DE=
BC．
（2）BF+BP=
DE．理由如下：
∵线段DP绕点D逆时针旋转60°，得到线段DF，∴∠PDF=60°，DP=DF，而∠CDB=60°，∴∠CDB﹣∠PDB=∠PDF﹣∠PDB，∴∠CDP=∠BDF．在△DCP和△DBF中，∵DC=DB，∠CDP=∠BDF，DP=DF，∴△DCP≌△DBF（SAS），∴CP=BF，而CP=BC﹣BP，∴BF+BP=BC．∵DE=
BC，∴BC=
DE，∴BF+BP=
DE．
灵星计算小达人系列答案
【题目】从甲、乙两名同学中选拔一人参加“中华好诗词”大赛，在相同的测试条件下，对两人进行了五次模拟，并对成绩（单位：分）进行了整理，计算出 
=83分， 
=82分，绘制成如下尚不完整的统计图表． 甲、乙两人模拟成绩统计表
① | ② | ③ | ④ | ⑤ | |
甲成绩/分 | 79 | 86 | 82 | a | 83 |
乙成绩/分 | 88 | 79 | 90 | 81 | 72 |
根据以上信息，回答下列问题：
（1）a=
（2）请完成图中表示甲成绩变化情况的折线． 
（3）经计算S甲2=6，S乙2=42，综合分析，你认为选拔谁参加比赛更合适，说明理由．
（4）如果分别从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析，求抽到的两个人的成绩都大于82分的概率．
