题目内容
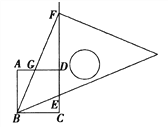
【题目】如图,一个Rt△DEF直角边DE落在AB上,过A点作射线AC与斜边EF平行,已知AB=12,DE=4,DF=3,点P从A点出发,沿射线AC方向以每秒2个单位的速度运动,Q为AP中点,设运动时间为t秒(t>0) 
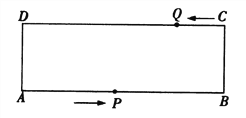
(1)若点D与点B重合,当t=5时,连接QE,PF,此时△AQE为三角形、四边形QEFP为形;
(2)如图②,若在点P运动时,Rt△DEF同时沿着BA方向以每秒1个单位的速度运动,当D点到A点时,两个运动都停止. ①如图①,若M为EF中点,当D、M、Q三点在同一直线上时,求t的值;
②在运动过程中,以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切时,求运动时间t.
【答案】
(1)等腰;菱
(2)解:①当D、M、Q三点在同一直线上时,如图②,
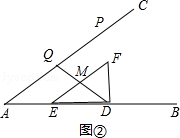
此时AQ=t,EM= ![]() EF=
EF= ![]() ,AD=12﹣t,DE=4.
,AD=12﹣t,DE=4.
∵EF∥AC,
∴△DEM∽△DAQ,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得t= ![]() ;
;
②存在以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切,
此时点Q在∠ADF的角平分线上或在∠FDB的角平分线上.
Ⅰ.当点Q在∠ADF的角平分线上时,
过点Q作QH⊥AB于H,如图③,
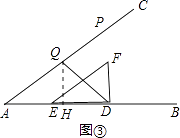
则有∠HQD=∠HDQ=45°,
∴QH=DH.
∵△AHQ∽△EDF(已证),
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴QH= ![]() ,AH=
,AH= ![]() ,
,
∴DH=QH= ![]() .
.
∵AB=AH+HD+BD=12,DB=t,
∴ ![]() +
+ ![]() +t=12,
+t=12,
∴t=5;
Ⅱ.当点Q在∠FDB的角平分线上时,
过点Q作QH⊥AB于H,如图④,
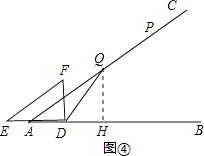
同理可得DH=QH= ![]() ,AH=
,AH= ![]() .
.
∵AB=AD+DB=AH﹣DH+DB=12,DB=t,
∴ ![]() ﹣
﹣ ![]() +t=12,
+t=12,
∴t=10.
综上所述:当t为5秒或10秒时,以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切.
【解析】解:(1)四边形EFPQ是菱形. 理由:过点Q作QH⊥AB于H,如图①,
∵t=5,∴AP=2×5=10.
∵点Q是AP的中点,
∴AQ=PQ=5.
∵∠EDF=90°,DE=4,DF=3,
∴EF= ![]() =5,
=5,
∴PQ=EF=5.
∵AC∥EF,
∴四边形EFPQ是平行四边形,且∠A=∠FEB.
又∵∠QHA=∠FDE=90°,
∴△AHQ∽△EDF,
∴ ![]() =
= ![]() =
= ![]() .
.
∵AQ=EF=5,
∴AH=ED=4.
∵AE=12﹣4=8,
∴HE=8﹣4=4,
∴AH=EH,
∴AQ=EQ,
∴PQ=EQ,
∴△AQE是等腰三角形,平行四边形EFPQ是菱形;
所以答案是:等腰,菱形.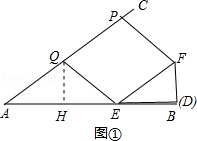

【题目】从甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,对两人进行了五次模拟,并对成绩(单位:分)进行了整理,计算出 ![]() =83分,
=83分, ![]() =82分,绘制成如下尚不完整的统计图表. 甲、乙两人模拟成绩统计表
=82分,绘制成如下尚不完整的统计图表. 甲、乙两人模拟成绩统计表
① | ② | ③ | ④ | ⑤ | |
甲成绩/分 | 79 | 86 | 82 | a | 83 |
乙成绩/分 | 88 | 79 | 90 | 81 | 72 |
根据以上信息,回答下列问题:
(1)a=
(2)请完成图中表示甲成绩变化情况的折线. 
(3)经计算S甲2=6,S乙2=42,综合分析,你认为选拔谁参加比赛更合适,说明理由.
(4)如果分别从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于82分的概率.