题目内容
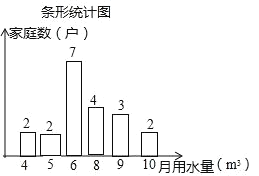
【题目】为进一步提高全民“节约用水”意识，某学校组织学生进行家庭月用水量情况调查活动，李明随机抽查了所住小区x户家庭的月用水量，绘制了下面不完整的统计图：
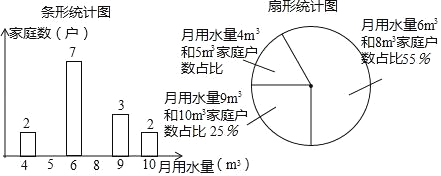
（1）求x并补全条形统计图；
（2）求这x户家庭的月平均用水量；并估计李明所住小区620户家庭中月用水量低于月平均用水量的家庭户数；
（3）从月用水量为5m3和9m3的家庭中任选两户进行用水情况问卷调查，求选出的两户中月用水量为5m3和9m3恰好各有一户家庭的概率；
【答案】（1）20，见解析；（2）6.95m3，低于月平均用水量的家庭户数约为231户；（3）
【解析】
(1）用水量为9和10的总户数除以它们所占的百分比得到x的值；再计算出月用水量8 m3的户数，月用水量5 m3的户数，然后补全条形统计图；
(2)先计算出这20户家庭的月平均用水量为6.95（m3），找出用水量低于6.95 m3的家庭户数为11，然后利用样本估计总体，用620乘以 
即可;
(3）画树状图展示所有20种等可能的结果数，找出选出的两户中月用水量为5 m3和9 m3恰好各有一户家庭的结果数，然后根据概率公式求解．
解：（1）x＝（3+2）÷25%＝20，
20×55%＝11，
月用水量8m3的户数为11﹣7＝4，
月用水量5m3的户数为20﹣2﹣7﹣4﹣3﹣2＝2，
（2）这20户家庭的月平均用水量为
（4×2+5×2+6×7+8×4+9×3+10×2）＝6.95（m3），
约用水量低于6.95m3的家庭共有11户，
所以620×＝341，
即估计李明所住小区620户家庭中月用水量低于月平均用水量的家庭户数约为231户；
（3）画树状图为：
共有20种等可能的结果数，选出的两户中月用水量为5m3和9m3恰好各有一户家庭的结果数为12，
所以选出的两户中月用水量为5m3和9m3恰好各有一户家庭的概率＝
=．
