题目内容
【题目】同时抛掷两枚质地均匀的正四面体骰子,骰子各个面的点数分别是1至4的整数,把这两枚骰子向下的面的点数记为(a,b),其中第一枚骰子的点数记为a,第二枚骰子的点数记为b.
(1)用列举法或树状图法求(a,b)的结果有多少种?
(2)求方程x2+bx+a=0有实数解的概率.
【答案】(1)一共有16种结果;(2)![]() .
.
【解析】
(1)根据题意画出树状图,得出所有等情况的结果数,再列举出来即可;
(2)先找出符合条件的结果数,再根据概率公式即可得出答案.
解:(1)根据题意画图如下:
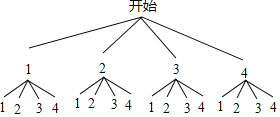
(a,b)的结果如下:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),一共有16种结果;
(2)易知方程是一元二次方程,其有解的条件是b2﹣4a≥0,
符合条件的(a,b):(1,4),(2,4),(3,4),(4,4),(1,3),(2,3),(1,2)共有7种结果,
所以,此方程有解的概率是![]() .
.

【题目】某校七年级计划成立学生社团,要求每一位学生都选择一个社团而且只能选择一个社团.为了解学生对不同社团的选择意向,随机抽取了七年级部分学生进行“我最喜爱的社团”问卷调查,并将调查结果绘制成如下两个不完整的统计图表.
七年级部分学生“我最喜爱的社团”调查结果统计表
社团名称 | 人数 |
文学社团 | 4 |
创客社团 | 9 |
书法社团 |
|
绘画社团 | 6 |
体育社团 | 10 |
音乐社团 | 5 |
美食社团 |
|
数学社团 | 2 |
七年级部分学生“我最喜爱的社团”调查结果扇形统计图
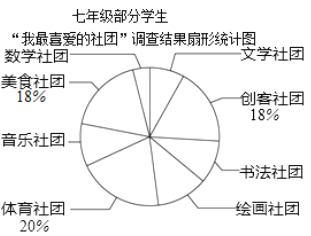
请解答下列问题:
(1)![]() ______,
______,![]() ______.
______.
(2)在扇形统计图中,“绘画社团”所对应的扇形圆心角为______度.
(3)该校七年级共有350名学生,每个社团人数不低于30人才可以开展.试通过计算估计该校七年级有哪些社团可以开展.