题目内容
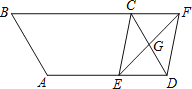
【题目】如图,直线y=-![]() x+2与x 轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y=
x+2与x 轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y=![]() (k<0)经过点B与直线CD交于E,EM⊥x轴于M,则SBEMC=______
(k<0)经过点B与直线CD交于E,EM⊥x轴于M,则SBEMC=______
【答案】![]()
【解析】
如图,直线![]() 与x轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线
与x轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线![]() (k<0)经过点B与直线CD交于E,EM⊥x轴于M,则S四边形BEMC=
(k<0)经过点B与直线CD交于E,EM⊥x轴于M,则S四边形BEMC=![]()
解:根据题意,直线![]() 与x轴交于C,与y轴交于D,
与x轴交于C,与y轴交于D,
分别令x=0,y=0,
得y=2,x=4,
即D(0,2),C(4,0),
即DC=![]() ,
,
又AD⊥DC且过点D,
所以直线AD所在函数解析式为:y=2x+2,
令y=0,得x=-1,
即A(-1,0),
同理可得B点的坐标为B(3,-2)
又B为双曲线![]() (k<0)上,
(k<0)上,
代入得k=-6.
即双曲线的解析式为![]()
与直线DC联立,
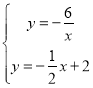
得x=6,y=-1和x=-2,y=3
根据题意,x=-2,y=3不合题意,
故点E的坐标为(6,-1).
所以BC=![]() ,CE=
,CE=![]() ,
,
CM=2,EM=1,
所以S△BEC=![]() ×BC×EC=
×BC×EC=![]()
S△EMC=![]() ×EM×CM=1,
×EM×CM=1,
故S四BEMC=S△BEC+S△EMC=![]() .
.

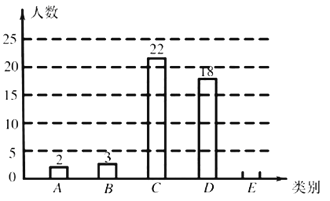
【题目】在推进城乡生活垃圾分类的行动中,某校数学兴趣小组为了了解居民掌握垃圾分类知识的情况,对![]() 两小区各600名居民进行测试,从中各随机抽取50名居民成绩进行整理得到部分信息:
两小区各600名居民进行测试,从中各随机抽取50名居民成绩进行整理得到部分信息:
(信息一)![]() 小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
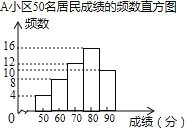
(信息二)上图中,从左往右第四组成绩如下:
75 | 77 | 77 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)![]() 两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | ___________ | 79 | 40% | 277 |
| 75.1 | 77 | 76 | 45% | 211 |
根据以上信息,回答下列问题:
(1)求![]() 小区50名居民成绩的中位数;
小区50名居民成绩的中位数;
(2)请估计![]() 小区600名居民成绩能超过平均数的人数;
小区600名居民成绩能超过平均数的人数;
(3)请尽量从多个角度,选择合适的统计量分析![]() 两小区参加测试的居民掌握垃圾分类知识的情况.
两小区参加测试的居民掌握垃圾分类知识的情况.