题目内容
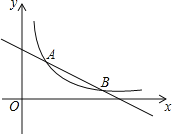
【题目】如图,抛物线![]() 的图象过点
的图象过点![]() .
.
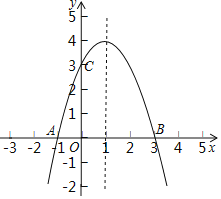
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点P,使得△PAC的周长最小,若存在,请求出点P的坐标及△PAC的周长;若不存在,请说明理由;
(3)在(2)的条件下,在x轴上方的抛物线上是否存在点M(不与C点重合),使得![]() ?若存在,请求出点M的坐标;若不存在,请说明理由.
?若存在,请求出点M的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,点
;(2)存在,点![]() ,周长为:
,周长为:![]() ;(3)存在,点M坐标为
;(3)存在,点M坐标为![]()
【解析】
(1)由于条件给出抛物线与x轴的交点![]() ,故可设交点式
,故可设交点式![]() ,把点C代入即求得a的值,减小计算量.
,把点C代入即求得a的值,减小计算量.
(2)由于点A、B关于对称轴:直线![]() 对称,故有
对称,故有![]() ,则
,则![]() ,所以当C、P、B在同一直线上时,
,所以当C、P、B在同一直线上时,![]() 最小.利用点A、B、C的坐标求AC、CB的长,求直线BC解析式,把
最小.利用点A、B、C的坐标求AC、CB的长,求直线BC解析式,把![]() 代入即求得点P纵坐标.
代入即求得点P纵坐标.
(3)由![]() 可得,当两三角形以PA为底时,高相等,即点C和点M到直线PA距离相等.又因为M在x轴上方,故有
可得,当两三角形以PA为底时,高相等,即点C和点M到直线PA距离相等.又因为M在x轴上方,故有![]() .由点A、P坐标求直线AP解析式,即得到直线CM解析式.把直线CM解析式与抛物线解析式联立方程组即求得点M坐标.
.由点A、P坐标求直线AP解析式,即得到直线CM解析式.把直线CM解析式与抛物线解析式联立方程组即求得点M坐标.
解:(1)∵抛物线与x轴交于点![]()
∴可设交点式![]()
把点![]() 代入得:
代入得:![]()
![]()
![]()
∴抛物线解析式为![]()
(2)在抛物线的对称轴上存在一点P,使得![]() 的周长最小.
的周长最小.
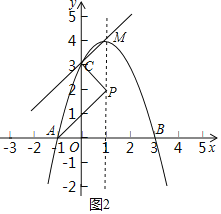
如图1,连接PB、BC
∵点P在抛物线对称轴直线![]() 上,点A、B关于对称轴对称
上,点A、B关于对称轴对称
![]()
![]()
∵当C、P、B在同一直线上时,![]() 最小
最小
![]()
![]()
![]() 最小
最小
设直线BC解析式为![]()
把点B代入得:![]() ,解得:
,解得:![]()
∴直线BC:![]()
![]()
∴点![]() 使
使![]() 的周长最小,最小值为
的周长最小,最小值为![]() .
.
(3)存在满足条件的点M,使得![]() .
.
∵![]() S△PAM=S△PAC
S△PAM=S△PAC
∴当以PA为底时,两三角形等高
∴点C和点M到直线PA距离相等
∵M在x轴上方
![]()
![]() ,设直线AP解析式为
,设直线AP解析式为![]()
![]() 解得:
解得:![]()
∴直线![]()
∴直线CM解析式为:![]()
![]()
解得:![]() (即点C),
(即点C),
∴点M坐标为![]()


 新思维寒假作业系列答案
新思维寒假作业系列答案【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | 200﹣2x |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.