题目内容
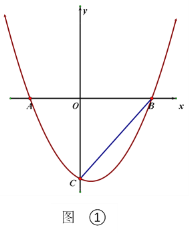
【题目】如图1，在平面直角坐标系中，直线y＝x+4与抛物线y＝﹣
x2+bx+c（b，c是常数）交于A、B两点，点A在x轴上，点B在y轴上．设抛物线与x轴的另一个交点为点C．
（1）求该抛物线的解析式；
（2）P是抛物线上一动点（不与点A、B重合），
①如图2，若点P在直线AB上方，连接OP交AB于点D，求
的最大值；
②如图3，若点P在x轴的上方，连接PC，以PC为边作正方形CPEF，随着点P的运动，正方形的大小、位置也随之改变．当顶点E或F恰好落在y轴上，直接写出对应的点P的坐标．
【答案】（1）
；（2）①
；②P点坐标（
，），（
，
），（
，2 ）（
，2 ）
【解析】
（1）利用直线解析式求出点A、B的坐标，再利用待定系数法求二次函数解析式即可；
（2）作PF∥BO交AB于点F，证△PFD∽△OBD，得比例线段
，则PF取最大值时，求得
的最大值；
（3）（i）点F在y轴上时，过点P作PH⊥x轴于H，根据正方形的性质可证明△CPH≌△FCO，根据全等三角形对应边相等可得PH=CO=2，然后利用二次函数解析式求解即可；（ii）点E在y轴上时，过点PK⊥x轴于K，作PS⊥y轴于S，同理可证得△EPS≌△CPK，可得PS=PK，则P点的横纵坐标互为相反数，可求出P点坐标；点E在y轴上时，过点PM⊥x轴于M，作PN⊥y轴于N，同理可证得△PEN≌△PCM，可得PN=PM，则P点的横纵坐标相等，可求出P点坐标．
解：（1）直线y＝x+4与坐标轴交于A、B两点，
当x＝0时，y＝4，x＝﹣4时，y＝0，
∴A（﹣4，0），B（0，4），
把A，B两点的坐标代入解析式得，
，解得，
，
∴抛物线的解析式为 ；
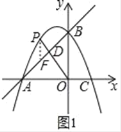
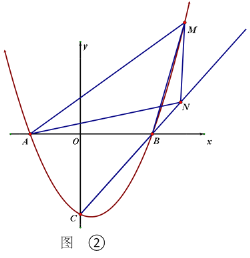
（2）①如图1，作PF∥BO交AB于点F，
∴△PFD∽△OBD，
∴，
∵OB为定值，
∴当PF取最大值时，有最大值，
设P（x，
），其中﹣4＜x＜0，则F（x，x+4），
∴PF＝
＝
，
∵
且对称轴是直线x＝﹣2，
∴当x＝﹣2时，PF有最大值，
此时PF＝2，
；
②∵点C（2，0），
∴CO＝2，
（i）如图2，点F在y轴上时，过点P作PH⊥x轴于H，
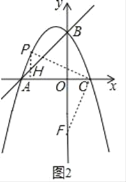
在正方形CPEF中，CP＝CF，∠PCF＝90°，
∵∠PCH+∠OCF＝90°，∠PCH+∠HPC＝90°，
∴∠HPC＝∠OCF，
在△CPH和△FCO中，
，
∴△CPH≌△FCO（AAS），
∴PH＝CO＝2，
∴点P的纵坐标为2，
∴
，
解得，
，
∴
，
，
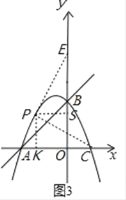
（ii）如图3，点E在y轴上时，过点PK⊥x轴于K，作PS⊥y轴于S，
同理可证得△EPS≌△CPK，
∴PS＝PK，
∴P点的横纵坐标互为相反数，
∴
，
解得x＝2
（舍去），x＝﹣2，
∴
，
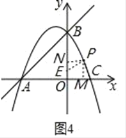
如图4，点E在y轴上时，过点PM⊥x轴于M，作PN⊥y轴于N，
同理可证得△PEN≌△PCM
∴PN＝PM，
∴P点的横纵坐标相等，
∴
，
解得
，
（舍去），
∴
，
综合以上可得P点坐标（，），（， ），（，2 ）（，2 ）．
