题目内容
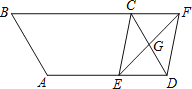
【题目】如图,![]() 是矩形
是矩形![]() 内的任意一点,连接
内的任意一点,连接![]() 、
、![]() 、
、![]() 、
、![]() , 得到
, 得到![]() ,
, ![]() ,
, ![]() ,
, ![]() ,设它们的面积分别是
,设它们的面积分别是![]() ,
,![]() ,
,![]() ,
,![]() , 给出如下结论:①
, 给出如下结论:①![]() ②
②![]() ③若
③若![]() ,则
,则![]() ④若
④若![]() ,则
,则![]() 点在矩形的对角线上.其中正确的结论的序号是( )
点在矩形的对角线上.其中正确的结论的序号是( )

A.①②B.②③C.③④D.②④
【答案】D
【解析】
根据三角形面积公式、矩形性质及相似多边形的性质得出:
①矩形对角线平分矩形,S△ABD=S△BCD,只有P点在BD上时,S +S =S +S4;
②根据底边相等的两个三角形的面积公式求和可知,S+S=![]() 矩形ABCD面积,同理S+S4=
矩形ABCD面积,同理S+S4=![]() 矩形ABCD面积,所以S+S= S+S4;
矩形ABCD面积,所以S+S= S+S4;
③根据底边相等高不相等的三角形面积比等于高的比来说明即可;
④根据相似四边形判定和性质,对应角相等、对应边成比例的四边形相似,矩形AEPF∽矩形ABCD推出![]() ,点P在对角线上.
,点P在对角线上.
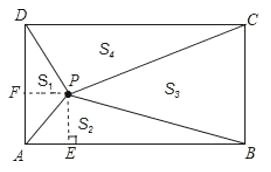
解:①当点P在矩形的对角线BD上时,S +S =S +S4.但P是矩形ABCD内的任意一点,所以该等式不一定成立。故①不一定正确;
②∵矩形![]()
∴AB=CD,AD=BC
∵△APD以AD为底边,△PBC以BC为底边,这两三角形的底相等,高的和为AB,
∴S +S =![]() S矩形ABCD;
S矩形ABCD;
同理可得S +S4=![]() S矩形ABCD ,
S矩形ABCD ,
∴②S+S4=S+S正确;
③若S =2S ,只能得出△APD与△PBC高度之比是![]() ,S、S4分别是以AB、CD为底的三角形的面积,底相等,高的比不一定等于
,S、S4分别是以AB、CD为底的三角形的面积,底相等,高的比不一定等于![]() ,S4=2S2不一定正确 ;故此选项错误;
,S4=2S2不一定正确 ;故此选项错误;
④过点P分别作PF⊥AD于点F,PE⊥AB于点E,F.
若S1=S2,.则![]() AD·PF=
AD·PF=![]() AB·PE
AB·PE
∴△APD与△PAB的高的比为:![]()
∵∠DAE=∠PEA=∠PFA =90°
∴四边形AEPF是矩形,
∴矩形AEPF∽矩形ABCD
∴![]()
∴P点在矩形的对角线上,选项④正确.
故选:D

【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且利润率不得高于![]() .经市场调查,每天的销售量
.经市场调查,每天的销售量![]() (千克)与每千克售价
(千克)与每千克售价![]() (元)满足一次函数关系,部分数据如下表:
(元)满足一次函数关系,部分数据如下表:
售价 | 45 | 50 | 55 |
销售量 | 110 | 100 | 90 |
(1)求![]() 与
与![]() 之间的函数表达式,并写出自变量的范围;
之间的函数表达式,并写出自变量的范围;
(2)设每天销售该商品的总利润为![]() (元),求
(元),求![]() 与
与![]() 之间的函数表达式(利润=收入-成本),并求出售价为多少元时每天销售该商品所获得最大利润,最大利润是多少?
之间的函数表达式(利润=收入-成本),并求出售价为多少元时每天销售该商品所获得最大利润,最大利润是多少?