题目内容
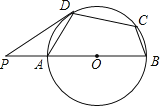
【题目】如图，AB为⊙O的直径，四边形ABCD为⊙O的内接四边形，点P在BA的延长线上，PD与⊙O相切，D为切点，若∠BCD＝125°，则∠ADP的大小为（ ）
A.25°B.40°C.35°D.30°
【答案】C
【解析】
连接AC，OD，根据直径所对的圆周角是直角得到∠ACB是直角，求出∠ACD的度数，根据圆周角定理求出∠AOD的度数，再利用切线的性质即可得到∠ADP的度数．
连接AC，OD．
∵AB是直径，
∴∠ACB=90°，
∴∠ACD=125°﹣90°=35°，
∴∠AOD=2∠ACD=70°．
∵OA=OD，
∴∠OAD=∠ADO，
∴∠ADO=55°．
∵PD与⊙O相切，
∴OD⊥PD，
∴∠ADP=90°﹣∠ADO=90°﹣55°=35°．
故选：C．
练习册系列答案
相关题目
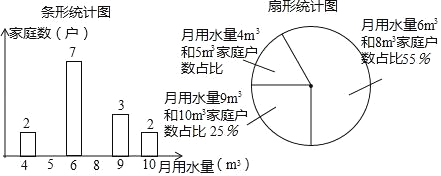
【题目】在推进城乡生活垃圾分类的行动中，某校数学兴趣小组为了了解居民掌握垃圾分类知识的情况，对
两小区各600名居民进行测试，从中各随机抽取50名居民成绩进行整理得到部分信息：
（信息一）
小区50名居民成绩的频数直方图如图（每一组含前一个边界值，不含后一个边界值）；
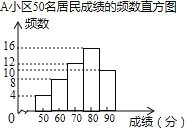
（信息二）上图中，从左往右第四组成绩如下：
75 | 77 | 77 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
（信息三）两小区各50名居民成绩的平均数、中位数、众数、优秀率（80分及以上为优秀）、方差等数据如下（部分空缺）：
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | ___________ | 79 | 40% | 277 |
| 75.1 | 77 | 76 | 45% | 211 |
根据以上信息，回答下列问题：
（1）求小区50名居民成绩的中位数；
（2）请估计小区600名居民成绩能超过平均数的人数；
（3）请尽量从多个角度，选择合适的统计量分析两小区参加测试的居民掌握垃圾分类知识的情况．
