题目内容
【题目】在一个不透明的盒子里装有3个分别写有数字﹣2，0，1的小球，它们除了数字不同以外其余完全相同，先从盒子里随机抽取1个小球，再从剩下的小球中抽取1个，将这两个小球上的数字依次记为a，b，则满足关于x的方程x2+ax+b＝0有实数根的概率为_____．
【答案】
．
【解析】
根据题意列表得出所有等可能的结果数，再找出满足△＝a2﹣4b≥0的结果数，然后根据概率公式求解即可．
解：列表如下
﹣2 | 0 | 1 | |
﹣2 | （0，﹣2） | （1，﹣2） | |
0 | （﹣2，0） | （1，0） | |
1 | （﹣2，1） | （0，1） |
由表知共有6种等可能结果，其中满足△＝a2﹣4b≥0的有（﹣2，0）、（﹣2，1）、（0，﹣2）、（1，﹣2）、（1，0）这5种结果，
∴满足关于x的方程x2+ax+b＝0有实数根的概率为
，
故答案为：．
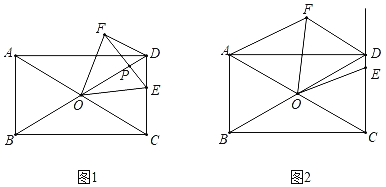
【题目】如图1，长度为6千米的国道
两侧有
，
两个城镇，从城镇到公路分别有乡镇公路连接，连接点为
和
，其中
、之间的距离为2千米，、之间的距离为1千米，、之间的乡镇公路长度为2.3千米，、之间的乡镇公路长度为3.2千米，为了发展乡镇经济，方便两个城镇的物资输送，现需要在国道上修建一个物流基地
，设、之间的距离为
千米，物流基地沿公路到、两个城镇的距离之和为
干米，以下是对函数随自变量的变化规律进行的探究，请补充完整．
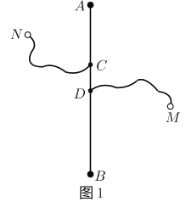
（1）通过取点、画图、测量，得到与的几组值，如下表：
| 0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| 10.5 | 8.5 | 6.5 | 10.5 | 12.5 |
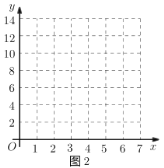
（2）如图2，建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象．
（3）结合画出的函数图象，解决问题：
①若要使物流基地沿公路到、两个城镇的距离之和最小，则物流基地应该修建在何处？（写出所有满足条件的位置）
答：__________．
②如右图，有四个城镇、、
、
分别位于国道
两侧，从城镇到公路分别有乡镇公路连接，若要在国道上修建一个物流基地
，使得沿公路到、、、的距离之和最小，则物流基地应该修建在何处？（写出所有满足条件的位置）
答：__________．
