题目内容
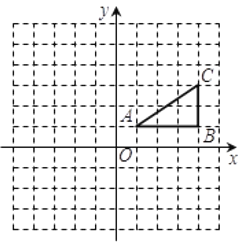
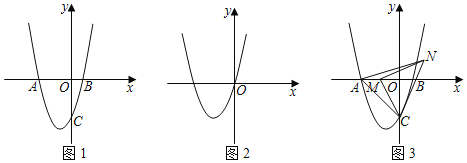
【题目】已知在平面直角坐标系中,抛物线y=x2+3x﹣a2+a+2(a>1)的图象交x轴于点A和点B(点A在点B左侧),与y轴交于点C,顶点为E.
(1)如图1,求线段AB的长度(用含a的式子表示)及抛物线的对称轴;
(2)如图2,当抛物线的图象经过原点时,在平面内是否存在一点P,使得以A、B、E、P为顶点的四边形能否成为平行四边形?如果能,求出P点坐标;如果不能,请说明理由;
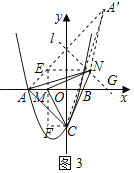
(3)如图3,当a=3时,若M点为x轴上一动点,连结MC,将线段MC绕点M逆时针旋转90°得到线段MN,连结AC、CN、AN,则△ACN周长的最小值为多少?
【答案】(1)AB=2a﹣1,抛物线的对称轴为x=﹣![]() ;(2)存在,P点坐标为(
;(2)存在,P点坐标为(![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() );(3)4
);(3)4![]() +4
+4![]() .
.
【解析】
(1)当y=0时,x2+3x﹣a2+a+2=0,则[x﹣(a﹣2)][x+(a+1)]=0,解得x=a﹣2,或x=﹣a﹣1,进而求出AB的长度和抛物线的对称轴;
(2)由抛物线的图象经过原点,a>1,得出a=2,此时A(﹣3,0),B(0,0),
E(-![]() ,﹣
,﹣![]() ),①若AB为平行四边形的边,则P点坐标为(
),①若AB为平行四边形的边,则P点坐标为(![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() );②若AB为平行四边形的对角线,则P点坐标为(﹣
);②若AB为平行四边形的对角线,则P点坐标为(﹣![]() ,﹣
,﹣![]() );
);
(3)当a=3时,y=x2+3x﹣4,设M(t,0),证△MNE≌△CMF(AAS),得出MF=CF=OM=﹣t,EN=MF=OC=4,证出点N在直线l:y=﹣x+4上运动,设直线l交x轴于点G,则G(4,0),若使△ACN的周长最小,即使AN+CN最小,作点A关于l的对称点A',连接A'C,则AN=A'N,得出AN+CN最小=A'C,求出AG=8,AA'=![]() ,AC=
,AC=![]() ,由勾股定理得出A'C=
,由勾股定理得出A'C=![]() ,进而得出答案.
,进而得出答案.
解:(1)当y=0时,x2+3x﹣a2+a+2=0,
∴[x﹣(a﹣2)][x+(a+1)]=0,
∴x=a﹣2,或x=﹣a﹣1,
∵点A在点B左侧,
∴A(﹣a﹣1,0),B(a﹣2,0),
∴AB=a﹣2﹣(﹣a﹣1)=2a﹣1,
抛物线的对称轴为x=![]() =﹣
=﹣![]() ,即抛物线的对称轴为x=﹣
,即抛物线的对称轴为x=﹣![]() ;
;
(2)存在,理由如下:
∵抛物线y=x2+3x﹣a2+a+2(a>1)的图象经过原点,a>1,
∴﹣a2+a+2=0,
解得:a=2,或a=﹣1(舍去),
∴a=2,
∴A(﹣3,0),B(0,0),y=x2+3x=(x+![]() )2﹣
)2﹣![]() ,
,
∴E(﹣![]() ,﹣
,﹣![]() ),
),
分情况讨论,如图2所示:
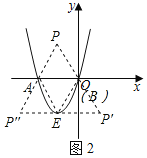
①若AB为平行四边形的边,则P点坐标为(![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() );
);
②若AB为平行四边形的对角线,则P点坐标为(﹣![]() ,﹣
,﹣![]() );
);
综上所述,在平面内存在一点P,使得以A、B、E、P为顶点的四边形成为平行四边形,P点坐标为(![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() );
);
(3)当a=3时,y=x2+3x﹣4,
此时A(﹣4,0),B(1,0),C(0,﹣4),
∴OA=4,OC=4,
设M(t,0),
∵将线段MC绕点M逆时针旋转90°得到线段MN,
∴OM=﹣t,
过点M作EF⊥x轴,过点N作NE⊥EF于点E,过点C作CF⊥EF于点F,如图3所示:
则∠MEN=∠CFM=90°,
由旋转的性质得:MN=MC,∠CMN=90°,
∴∠EMN+∠CMF=∠CMF+∠FCM=90°,
∴∠EMN=∠FCM,
在△MNE和△CMF中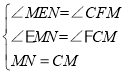 ,
,
∴△MNE≌△CMF(AAS),
∴MF=CF=OM=﹣t,EN=MF=OC=4,
∴点N的横坐标为Nx=4+t,点N的纵坐标为Ny=﹣t,
∴y=﹣x+4,
∴点N在直线l:y=﹣x+4上运动,
设直线l交x轴于点G,则G(4,0),
若使△ACN的周长最小,即使AN+CN最小,
∴作点A关于l的对称点A',连接A'C,A'N,
则AN=A'N,
当A'、N、C三点共线时,AN+CN最小=A'C,
由题意得:∠A'AO=45°,∠CAO=45°,
∴∠CAA'=90°,
∵G(4,0),
∴AG=OA+OG=8,AA'=![]() ,
,
∵AC=![]() =
=![]() ,
,
∴A'C=![]() =
=![]() ,
,
∴A'C+AC=![]() +
+![]() ,
,
∵△ACN的周长=AN+CN+AC,
∴△ACN周长的最小值为A'C+AC=4![]() +4
+4![]() .
.