ЬтФПФкШн
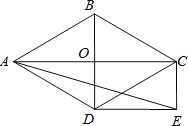
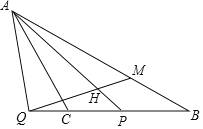
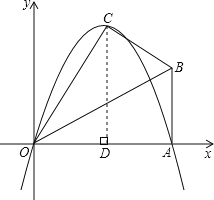
ЁОЬтФПЁПвбжЊЃЎдкRtЁїOABжаЃЌЁЯOAB=90ЁуЃЌЁЯBOA=30ЁуЃЌOA=2![]() ЃЌШєвдOЮЊзјБъдЕуЃЌOAЫљдкжБЯпЮЊxжсЃЌНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЌЕуBдкЕквЛЯѓЯоФкЃЌНЋRtЁїOABбиOBелЕўКѓЃЌЕуAТфдкЕквЛЯѓЯоФкЕФЕуCДІЃЎ
ЃЌШєвдOЮЊзјБъдЕуЃЌOAЫљдкжБЯпЮЊxжсЃЌНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЌЕуBдкЕквЛЯѓЯоФкЃЌНЋRtЁїOABбиOBелЕўКѓЃЌЕуAТфдкЕквЛЯѓЯоФкЕФЕуCДІЃЎ

ЃЈ1ЃЉЧѓОЙ§ЕуOЃЌCЃЌAШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉШєЕуMЪЧХзЮяЯпЩЯвЛЕуЃЌЧвЮЛгкЯпЖЮOCЕФЩЯЗНЃЌСЌНгMOЁЂMCЃЌЮЪЃКЕуMЮЛгкКЮДІЪБШ§НЧаЮMOCЕФУцЛ§зюДѓЃПВЂЧѓГіШ§НЧаЮMOCЕФзюДѓУцЛ§ЃЎ
ЃЈ3ЃЉХзЮяЯпЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЁЯOAP=ЁЯBOCЃПШєДцдкЃЌЧыЧѓГіДЫЪБЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=Љx2+2![]() xЃЛЃЈ2ЃЉ
xЃЛЃЈ2ЃЉ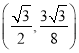 ,
,![]() ЃЛЃЈ3ЃЉДцдкЃЌP(
ЃЛЃЈ3ЃЉДцдкЃЌP(![]() ЃЌ
ЃЌ![]() )Лђ(Љ
)Лђ(Љ![]() ЃЌЉ
ЃЌЉ![]() )
)
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнелЕўЕФаджЪПЩЕУOC=OAЃЌЁЯBOC=ЁЯBAO=30ЁуЃЌЙ§ЕуCзїCDЁЭOAгкDЃЌЧѓГіODЁЂCDЃЌШЛКѓаДГіЕуCЕФзјБъЃЌдйРћгУД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§НтЮіЪННтД№ЃЛ
ЃЈ2ЃЉЧѓГіжБЯпOCЕФНтЮіЪНЃЌИљОнЕуMЕНOCЕФзюДѓОрРыЪБЃЌУцЛ§зюДѓЃЛЦНаагкOCЕФжБЯпгыХзЮяЯпжЛгавЛИіНЛЕуЃЌРћгУИљЕФХаБ№ЪНЧѓГіmЕФжЕЃЌРћгУШёНЧШ§НЧКЏЪ§ЕФЖЈвхЧѓНтМДПЩЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЧѓГіжБЯпAPгыyжсЕФНЛЕузјБъЃЌШЛКѓЧѓГіжБЯпAPЕФНтЮіЪНЃЌгыХзЮяЯпНтЮіЪНСЊСЂЧѓНтМДПЩЕУЕНЕуPЕФзјБъЃЎ
НтЃКЃЈ1ЃЉЁпRtЁїOABбиOBелЕўКѓЃЌЕуAТфдкЕквЛЯѓЯоФкЕФЕуCДІЃЌ
ЁрOC=OA=2![]() ЃЌЁЯBOC=ЁЯBAO=30ЁуЃЌ
ЃЌЁЯBOC=ЁЯBAO=30ЁуЃЌ
ЁрЁЯAOC=30Ёу+30Ёу=60ЁуЃЌ
Й§ЕуCзїCDЁЭOAгкDЃЌ
дђOD=![]() ЁС2
ЁС2![]() =
=![]() ЃЌ
ЃЌ
CD=2![]() ЁС
ЁС![]() =3ЃЌ
=3ЃЌ
ЫљвдЃЌЖЅЕуCЕФзјБъЮЊЃЈ![]() ЃЌ3ЃЉЃЌ
ЃЌ3ЃЉЃЌ
ЩшЙ§ЕуOЃЌCЃЌAХзЮяЯпЕФНтЮіЪНЮЊЮЊy=ax2+bxЃЌ
дђ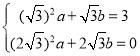 ЃЌ
ЃЌ
НтЕУЃК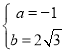 ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=Љx2+2![]() xЃЛ
xЃЛ
ЃЈ2ЃЉЁпCЃЈ![]() ЃЌ3ЃЉЃЌ
ЃЌ3ЃЉЃЌ
ЁржБЯпOCЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
ЩшЕуMЕНOCЕФзюДѓОрРыЪБЃЌЦНаагкOCЕФжБЯпНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
СЊСЂ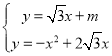 ЃЌ
ЃЌ
ЯћЕєЮДжЊЪ§yВЂећРэЕУЃЌ![]() ЃЌ
ЃЌ
Ёї=ЃЈ![]() ЃЉ2-4m=0ЃЌ
ЃЉ2-4m=0ЃЌ
НтЕУЃКm=![]() ЃЎ
ЃЎ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЁрЕуMЕНOCЕФзюДѓОрРы=![]() ЁСsin30Ёу=
ЁСsin30Ёу=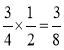 ЃЛ
ЃЛ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ДЫЪБЃЌM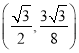 ЃЌзюДѓУцЛ§ЮЊ
ЃЌзюДѓУцЛ§ЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЁпЁЯOAP=ЁЯBOC=ЁЯBOA =30ЁуЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁржБЯпAPгыyжсЕФНЛЕузјБъЮЊЃЈ0ЃЌ2ЃЉЛђЃЈ0ЃЌЉ2ЃЉЃЌ
ЕБжБЯпAPОЙ§ЕуЃЈ![]() ЃЌ0ЃЉЁЂЃЈ0ЃЌ2ЃЉЪБЃЌНтЮіЪНЮЊ
ЃЌ0ЃЉЁЂЃЈ0ЃЌ2ЃЉЪБЃЌНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
СЊСЂ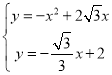 ЃЌ
ЃЌ
НтЕУ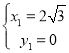 ЃЌ
ЃЌ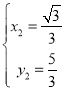 ЃЎ
ЃЎ
ЫљвдЕуPЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЕБжБЯпAPОЙ§ЕуЃЈ![]() ЃЌ0ЃЉЁЂЃЈ0ЃЌЉ2ЃЉЪБЃЌНтЮіЪНЮЊ
ЃЌ0ЃЉЁЂЃЈ0ЃЌЉ2ЃЉЪБЃЌНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
СЊСЂ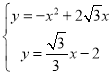
НтЕУ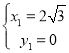 ЃЌ
ЃЌ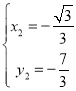 ЃЛ
ЃЛ
ЫљвдЕуPЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
злЩЯЫљЪіЃЌДцдквЛЕуPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈЉ
ЃЉЛђЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌЪЙЁЯOAP=ЁЯBOAЃЎ
ЃЉЃЌЪЙЁЯOAP=ЁЯBOAЃЎ