题目内容
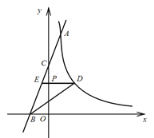
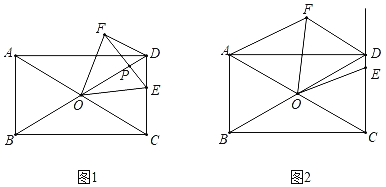
【题目】如图1,在矩形ABCD中,AB=1,对角线AC,BD相交于点O,∠COD=60°,点E是线段CD上一点,连接OE,将线段OE绕点O逆时针旋转60°得到线段OF,连接DF.
(1)求证:DF=CE;
(2)连接EF交OD于点P,求DP的最大值;
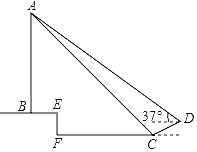
(3)如图2,点E在射线CD上运动,连接AF,在点E的运动过程中,若AF=AB,求OF的长.
【答案】(1)详见解析;(2)![]() ;(3)OF=1或
;(3)OF=1或![]() .
.
【解析】
(1)证明△FOD≌△EOC(SAS),则可得出结论;
(2)证明△FDP∽△ODE,可得出![]() ,设DF=CE=x,则DE=1﹣x,则
,设DF=CE=x,则DE=1﹣x,则![]() ,得出DP=﹣x2+x=
,得出DP=﹣x2+x=![]() ,由二次函数的性质可得出答案;
,由二次函数的性质可得出答案;
(3)分情况讨论:①如图1,过点F作FM⊥AD于点M,证明△AOF是等边三角形,得出OF=1;②过点A作AN⊥DF于点N,则∠FDA=30°,证明△OAF≌△AOD(SAS),得出OF=AD=![]() .
.
(1)证明:由题意知∠FOE=∠DOC=60°,
∴∠FOE﹣∠DOE=∠DOC﹣∠DOE,即∠FOD=∠EOC,
在矩形ABCD中,AC=BD=2OC=2OD,
∴OC=OD,
又∵OF=OE,
∴△FOD≌△EOC(SAS),
∴DF=CE;
(2)解:在△ODC中,OD=OC,∠COD=60°,
∴△OCD是等边三角形,∠OCD=60°,
又△FOD≌△EOC,
∴∠FDO=∠ECO=60°,
在△OEF中,OE=OF,∠EOF=60°,
∴△OEF是等边三角形,∠OEF=60°,
∴180°﹣∠FDP﹣∠FPD=180°﹣∠OEP﹣∠OPE,即∠DFP=∠DOE,
又∠FDP=∠ODE=60°,
∴△FDP∽△ODE,
∴![]() ,
,
设DF=CE=x,则DE=1﹣x,
∴![]() ,
,
∴DP=﹣x2+x=![]() ,
,
∴DP的最大值为![]() ;
;
(3)解:①在矩形ABCD中,AB=1,∠COD=60°,
∴AD=![]() ,∠OAD=∠ODA=30°,
,∠OAD=∠ODA=30°,
∴∠FDA=∠FDO﹣∠ODA=30°,
如图1,过点F作FM⊥AD于点M,
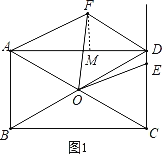
设FM=m,则MD=![]() m,AM=
m,AM=![]() -
-![]() m,
m,
又∵AF=AB=1,
∴在Rt△AFM中,AM2+FM2=AF2,
∴![]() ,
,
∴m1=![]() ,m2=1(舍去),
,m2=1(舍去),
∴sin∠FAM=![]() ,
,
∴∠FAM=30°,
∴∠FAO=60°,且AF=AB=AO,
∴△AOF是等边三角形,
∴OF=1;
②如图2,过点A作AN⊥DF于点N,则∠FDA=30°,
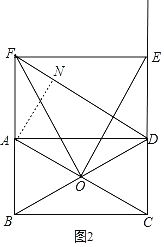
∴∠DAN=60°,AN=![]() ,
,
∴cos∠FAN=![]() ,
,
∴∠FAN=30°,
∴∠FAO=120°,
又∠AOD=120°,
∴∠FAO=∠AOD,
又AF=AO=OD,
∴△OAF≌△AOD(SAS),
∴OF=AD=![]() .
.
综合以上可得,OF=1或![]() .
.

 步步高达标卷系列答案
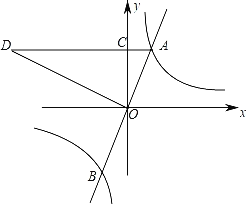
步步高达标卷系列答案【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图像交于点
的图像交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值和反比例函数的表达式;
的值和反比例函数的表达式;
(2)在![]() 轴上有一动点
轴上有一动点![]()
![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交反比例函数的图像于点
轴的直线,交反比例函数的图像于点![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,求
,求![]() 的值.
的值.