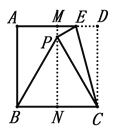ƒøƒ⁄»ð
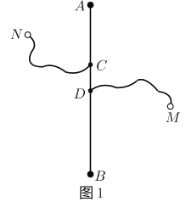
°æƒø°ø»ÁÕº1£¨≥§∂»Œ™6«ß√◊µƒπ˙µ¿![]() ¡Ω≤ý”–
¡Ω≤ý”–![]() £¨
£¨![]() ¡Ω∏ˆ≥«’Ú£¨¥”≥«’ÚµΩπ´¬∑∑÷±”–œÁ’Úπ´¬∑¡¨Ω”£¨¡¨Ω”µ„Œ™
¡Ω∏ˆ≥«’Ú£¨¥”≥«’ÚµΩπ´¬∑∑÷±”–œÁ’Úπ´¬∑¡¨Ω”£¨¡¨Ω”µ„Œ™![]() ∫Õ
∫Õ![]() £¨∆‰÷–
£¨∆‰÷–![]() °¢
°¢![]() ÷ƺ‰µƒæý¿ÎŒ™2«ß√◊£¨
÷ƺ‰µƒæý¿ÎŒ™2«ß√◊£¨![]() °¢
°¢![]() ÷ƺ‰µƒæý¿ÎŒ™1«ß√◊£¨
÷ƺ‰µƒæý¿ÎŒ™1«ß√◊£¨![]() °¢
°¢![]() ÷ƺ‰µƒœÁ’Úπ´¬∑≥§∂»Œ™2.3«ß√◊£¨
÷ƺ‰µƒœÁ’Úπ´¬∑≥§∂»Œ™2.3«ß√◊£¨![]() °¢
°¢![]() ÷ƺ‰µƒœÁ’Úπ´¬∑≥§∂»Œ™3.2«ß√◊£¨Œ™¡À∑¢’πœÁ’Úæ≠º√£¨∑Ω±„¡Ω∏ˆ≥«’ÚµƒŒÔ◊ ‰ÀÕ£¨œ÷–Ë“™‘⁄π˙µ¿
÷ƺ‰µƒœÁ’Úπ´¬∑≥§∂»Œ™3.2«ß√◊£¨Œ™¡À∑¢’πœÁ’Úæ≠º√£¨∑Ω±„¡Ω∏ˆ≥«’ÚµƒŒÔ◊ ‰ÀÕ£¨œ÷–Ë“™‘⁄π˙µ¿![]() …œ–ÞΩ®“ª∏ˆŒÔ¡˜ª˘µÿ
…œ–ÞΩ®“ª∏ˆŒÔ¡˜ª˘µÿ![]() £¨…Ë
£¨…Ë![]() °¢
°¢![]() ÷ƺ‰µƒæý¿ÎŒ™
÷ƺ‰µƒæý¿ÎŒ™![]() «ß√◊£¨ŒÔ¡˜ª˘µÿ
«ß√◊£¨ŒÔ¡˜ª˘µÿ![]() —ÿπ´¬∑µΩ
—ÿπ´¬∑µΩ![]() °¢
°¢![]() ¡Ω∏ˆ≥«’Úµƒæý¿Î÷Æ∫ÕŒ™
¡Ω∏ˆ≥«’Úµƒæý¿Î÷Æ∫ÕŒ™![]() ∏…√◊£¨“‘œ¬ «∂‘∫Ø ˝
∏…√◊£¨“‘œ¬ «∂‘∫Ø ˝![]() ÀÊ◊‘±‰¡ø
ÀÊ◊‘±‰¡ø![]() µƒ±‰ªØπʬ…Ω¯––µƒÃΩæø£¨«Î≤π≥‰ÕÍ’˚£Æ
µƒ±‰ªØπʬ…Ω¯––µƒÃΩæø£¨«Î≤π≥‰ÕÍ’˚£Æ
£®1£©Õ®π˝»°µ„°¢ª≠Õº°¢≤‚¡ø£¨µ√µΩ![]() ”Î
”Î![]() µƒº∏◊È÷µ£¨»Áœ¬±Ì£∫
µƒº∏◊È÷µ£¨»Áœ¬±Ì£∫
| 0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| 10.5 | 8.5 | 6.5 | 10.5 | 12.5 |
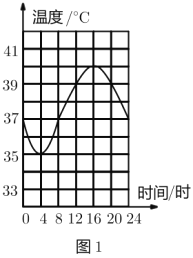
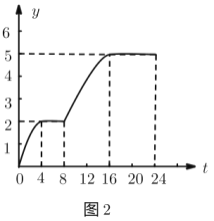
£®2£©»ÁÕº2£¨Ω®¡¢∆Ω√Ê÷±Ω«◊¯±Íœµ£¨√Ë≥ˆ“‘≤π»´∫Ûµƒ±Ì÷–∏˜∂‘∂‘”¶÷µŒ™◊¯±Íµƒµ„£¨ª≠≥ˆ∏√∫Ø ˝µƒÕºœÛ£Æ
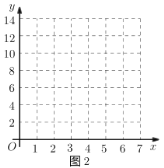
£®3£©Ω·∫œª≠≥ˆµƒ∫Ø ˝ÕºœÛ£¨Ω‚戌 £∫
¢Ÿ»Ù“™ πŒÔ¡˜ª˘µÿ![]() —ÿπ´¬∑µΩ
—ÿπ´¬∑µΩ![]() °¢
°¢![]() ¡Ω∏ˆ≥«’Úµƒæý¿Î÷Æ∫Õ◊Ó–°£¨‘ڌԡ˜ª˘µÿ
¡Ω∏ˆ≥«’Úµƒæý¿Î÷Æ∫Õ◊Ó–°£¨‘ڌԡ˜ª˘µÿ![]() ”¶∏√–ÞΩ®‘⁄∫Œ¥¶£ø£®–¥≥ˆÀ˘”–¬˙◊„Ãıº˛µƒŒª÷√£©
”¶∏√–ÞΩ®‘⁄∫Œ¥¶£ø£®–¥≥ˆÀ˘”–¬˙◊„Ãıº˛µƒŒª÷√£©
¥£∫__________£Æ
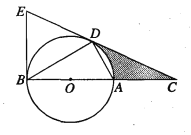
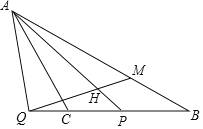
¢⁄»Á”“Õº£¨”–Àƒ∏ˆ≥«’Ú![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() ∑÷±Œª”⁄π˙µ¿
∑÷±Œª”⁄π˙µ¿![]() ¡Ω≤ý£¨¥”≥«’ÚµΩπ´¬∑∑÷±”–œÁ’Úπ´¬∑¡¨Ω”£¨»Ù“™‘⁄π˙µ¿…œ–ÞΩ®“ª∏ˆŒÔ¡˜ª˘µÿ
¡Ω≤ý£¨¥”≥«’ÚµΩπ´¬∑∑÷±”–œÁ’Úπ´¬∑¡¨Ω”£¨»Ù“™‘⁄π˙µ¿…œ–ÞΩ®“ª∏ˆŒÔ¡˜ª˘µÿ![]() £¨ πµ√
£¨ πµ√![]() —ÿπ´¬∑µΩ
—ÿπ´¬∑µΩ![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() µƒæý¿Î÷Æ∫Õ◊Ó–°£¨‘ڌԡ˜ª˘µÿ
µƒæý¿Î÷Æ∫Õ◊Ó–°£¨‘ڌԡ˜ª˘µÿ![]() ”¶∏√–ÞΩ®‘⁄∫Œ¥¶£ø£®–¥≥ˆÀ˘”–¬˙◊„Ãıº˛µƒŒª÷√£©
”¶∏√–ÞΩ®‘⁄∫Œ¥¶£ø£®–¥≥ˆÀ˘”–¬˙◊„Ãıº˛µƒŒª÷√£©
¥£∫__________£Æ

°æ¥∞∏°ø£®1£©6.5£¨8.5£ª£®2£©º˚Ω‚Œˆ£ª£®3£©¢Ÿ![]() ÷ƺ‰£¨¢⁄µ„
÷ƺ‰£¨¢⁄µ„![]() ¥¶
¥¶
°æΩ‚Œˆ°ø
£®1£©”…“‚∑÷x=2“‘º∞x=4¡Ω÷÷«Èøˆ∑÷ŒˆÃ÷¬€£¨≤¢Ω´œýπÿœþ∂Œµƒ≥§¥˙»Îº¥ø…µ√¥∞∏£ª
£®2£©∏˘æð±Ì∏Ò ˝æðœ»√˵„‘Ÿ¡¨Ω”ª≠≥ˆ∫Ø ˝ÕºœÛº¥ø…£ª
£®3£©¢Ÿ”…Õº–Œø…÷™£¨»ÙŒÔ¡˜ª˘µÿ–ÞΩ®‘⁄C°¢D¡Ωµ„÷ÆÕ‚£¨‘Úæý¿Îª·¥Û”⁄NC+CD+DM£¨¥”∂¯ø…µ√¥∞∏£ª
¢⁄Ω·∫œ¢ŸµƒΩ·¬€º∞–ÞΩ®‘⁄![]() …œ ±£¨µΩ
…œ ±£¨µΩ![]() °¢
°¢![]() ¡Ω∏ˆ≥«’Úµƒæý¿Î÷Æ∫Õ◊Ó–°◊€∫œ∑÷Œˆø…µ√¥∞∏£Æ
¡Ω∏ˆ≥«’Úµƒæý¿Î÷Æ∫Õ◊Ó–°◊€∫œ∑÷Œˆø…µ√¥∞∏£Æ
Ω‚£∫£®1£©µ±![]() ±£¨µ„
±£¨µ„![]() ‘⁄µ„
‘⁄µ„![]() ¥¶£¨
¥¶£¨
¥À ±![]() £ª
£ª
µ±![]() ±£¨µ„
±£¨µ„![]() ‘⁄µ„
‘⁄µ„![]() øøΩ¸
øøΩ¸![]() ≤ý1
≤ý1![]() ¥¶£¨
¥¶£¨
¥À ±![]() £Æ
£Æ
£®2£©√˵„£¨ª≠Õº»Áœ¬£∫
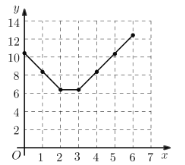
£®3£©¢Ÿ”…∫Ø ˝ÕºœÛø…µ√£¨µ±ŒÔ¡˜ª˘µÿ![]() ‘⁄
‘⁄![]() ÷ƺ‰ ±£¨—ÿπ´¬∑µΩ
÷ƺ‰ ±£¨—ÿπ´¬∑µΩ![]() °¢
°¢![]() ¡Ω∏ˆ≥«’Úµƒæý¿Î÷Æ∫Õ◊Ó–°£Æ
¡Ω∏ˆ≥«’Úµƒæý¿Î÷Æ∫Õ◊Ó–°£Æ
¢⁄µ±–ÞΩ®‘⁄![]() …œ ±£¨µΩ
…œ ±£¨µΩ![]() °¢
°¢![]() ¡Ω∏ˆ≥«’Úµƒæý¿Î÷Æ∫Õ◊Ó–°£ª
¡Ω∏ˆ≥«’Úµƒæý¿Î÷Æ∫Õ◊Ó–°£ª
µ±–ÞΩ®‘⁄![]() …œ ±£¨µΩ
…œ ±£¨µΩ![]() °¢
°¢![]() ¡Ω∏ˆ≥«’Úµƒæý¿Î÷Æ∫Õ◊Ó–°£ª
¡Ω∏ˆ≥«’Úµƒæý¿Î÷Æ∫Õ◊Ó–°£ª
◊€…œ£¨–ÞΩ®‘⁄µ„![]() ¥¶£¨‘ÚµΩ
¥¶£¨‘ÚµΩ![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() µƒæý¿Î÷Æ∫Õ◊Ó–°£Æ
µƒæý¿Î÷Æ∫Õ◊Ó–°£Æ

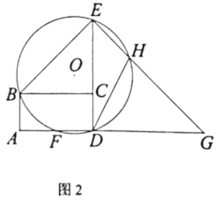
°æƒø°øƒ≥∆π≈“«Úπð π”√∑¢«Úª˙Ω¯––∏®÷˙—µ¡∑£¨≥ˆ«Úø⁄‘⁄◊¿√Ê÷–œþ∂Àµ„A¥¶µƒ’˝…œ∑Ω£¨ºŸ…Ë√ø¥Œ∑¢≥ˆµƒ∆π≈“«Úµƒ‘À∂ج∑œþπÃ∂®≤ª±‰£¨«“¬‰‘⁄÷–œþ…œ£¨‘⁄∆π≈“«Ú‘À–– ±£¨…Ë∆π≈“«Ú”Î∂Àµ„AµƒÀÆ∆Ωæý¿ÎŒ™x£®√◊£©£¨”Î◊¿√ʵƒ∏þ∂»Œ™y£®√◊£©£¨æ≠∂ý¥Œ≤‚ ‘∫Û£¨µ√µΩ»Áœ¬≤ø∑÷ ˝æð£∫
x/√◊ | 0 | 0.2 | 0.4 | 0.6 | 1 | 1.4 | 1.6 | 1.8 | °≠ |
y/√◊ | 0.24 | 0.33 | 0.4 | 0.45 | 0.49 | 0.45 | 0.4 | 0.33 | °≠ |
£®1£©”…±Ì÷–µƒ ˝æðº∞∫Ø ˝—ßœ∞æ≠—È£¨«Û≥ˆyπÿ”⁄xµƒ∫Ø ˝Ω‚Œˆ Ω£ª
£®2£© ‘«Û≥ˆµ±∆π≈“«Ú¬‰‘⁄◊¿√Ê ±£¨∆‰¬‰µ„”Î∂Àµ„AµƒÀÆ∆Ωæý¿Î «∂ý…Ÿ√◊£ø
£®3£©µ±∆π≈“«Ú¬‰‘⁄◊¿√Ê…œµØ∆∫Û£¨y”Îx÷ƺ‰¬˙◊„![]() £Æ
£Æ
¢Ÿ”√∫¨aµƒ¥˙ ˝ Ω±Ì æk£ª
¢⁄“—÷™«ÚÕ¯∏þ∂»Œ™0.14√◊£¨«Ú◊¿≥§£®1.4°¡2£©√◊£Æ»Ùa=-0.5£¨ƒ«√¥∆π≈“«ÚµØ∆∫Û£¨ «∑Ò”–ª˙ª·‘⁄ƒ≥∏ˆª˜«Úµ„ø…“‘Ω´«Ú—ÿ÷±œþø€…±µΩ∂Àµ„A£ø«ÎÀµ√˜¿Ì”…£Æ