Question

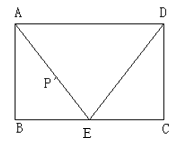
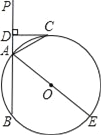
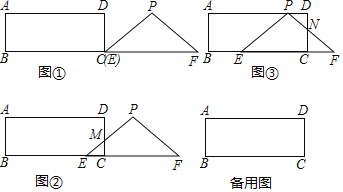
【题目】已知：Rt△EFP和矩形ABCD如图①摆放（点C与点E重合），点B，C（E），F在同一直线上，AB=3cm，BC=9cm，EF=8cm，PE=PF=5cm，如图②，△EFP从图①的位置出发，沿CB方向匀速运动，速度为2cm/s，当点F与点C重合时△EFP停止运动停止．设运动时间为t（s）（0＜t＜4），解答下列问题：

（1）当0＜t＜2时，EP与CD交于点M，请用含t的代数式表示CE=______，CM=______；

（2）当2＜t＜4时，如图③，PF与CD交于点N，设四边形EPNC的面积为y（cm2），求y与t之间的函数关系式；

（3）当2＜t＜4时，且S四边形EPNC：S矩形ABCD=1：4时，请求出t的值；

（4）连接BD，在运动过程中，当BD与EP相交时，设交点为O，当t=______时；O在∠BAD的平分线上．（不需要写解答过程）

Answer 1

【答案】（1）2t ， t ；（2）y=-t2+12t-12；（3）t=4 - ；（4）.

【解析】

（1）由等腰三角形的性质可得PH=3cm，EH=HF=4cm，由题意可得EC=2t，由锐角三角形函数可得tan∠PEH=，可得MC=t；

（2）由锐角三角函数可得CN=，由S△PEF-S△CNF=S四边形EPNC，可求y与t之间的函数关系式；

（3）由题意可得y=，代入解析式可求t的值；

（4）过点O作OM⊥AD，ON⊥AB，垂足分别为点M，点N，可得四边形ANOM是矩形，可得AM=ON，由角平分线的性质可得OM=ON，由三角形的面积关系可得ON=OM==AM，由锐角三角函数和平行线分线段成比例可求EC的长，即可求t的值．

解：（1）如图，过点P作PH⊥EF，垂足为H，

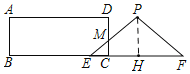
∵EF=8cm，PE=PF=5cm，PH⊥EF，

∴EH=HF=4cm，

∴PH==3cm，

∵△EFP沿CB方向匀速运动，速度为2cm/s，

∴CE=2t，

∵tan∠PEH=

∴

∴MC=t，

故答案为：2t，t，

（2）如图，过点P作PH⊥BC于点H，

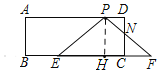
由（1）可知：PH=3cm，EH=HF=4cm，

∴S△PEF=×8×3=12，

∵CF=EF-EC，

∴CF=8-2t，

∵tan∠PFE=，

∴CN=，

∴y=S△PEF-S△CNF=12-×（8-2t）×（8-2t）=-t2+12t-12

（3）∵S四边形EPNC：S矩形ABCD=1：4

∴×3×9=-t2+12t-12

∴2t2-16t+25=0

∴t=4±

∵2＜t＜4

∴t=4-

（4）如图，过点O作OM⊥AD，ON⊥AB，垂足分别为点M，点N，

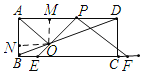
∵OM⊥AD，ON⊥AB，∠BAD=90°，

∴四边形ANOM是矩形，

∴AM=ON，

∵AO平分∠DAB，OM⊥AD，ON⊥AB，

∴OM=ON，

∵S△ABD=S△ABO+S△AOD，

∴

∴ON=OM==AM，

∵AD∥BC

∴∠APE=∠PEC

∵tan∠APE=tan∠PEC==

∴MP=3，

∴PD=AD-AM-MP=

∵ON∥AD

∴

∴

∵AD∥BC

∴

∴BE=PD=

∴EC=BC-EB=

∴t==

故答案为：