题目内容
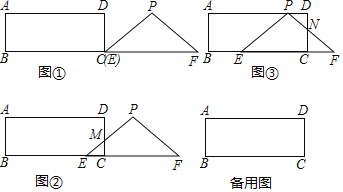
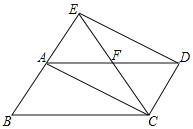
【题目】如图,将ABCD沿其对角线AC折叠,使△ABC落在AEC处,CE与AD交于点F,连接DE.
(1)请你判断AC,DE的位置关系,并说明理由;
(2)若折叠后,CE平分AD,AB=4,BC=6,请利用(1)中的结论,求ABCD的面积.
【答案】(1)见解析;(2) 8![]() .
.
【解析】
(1)先根据折叠的性质和平行四边形的性质判定△ACE≌△CAD,从而得到AF=CF,EF=DF,进而得出∠DEF=∠ACF,可得AC∥DE;
(2)先判定四边形ACDE是矩形,即可得到∠CAE=90°=∠BAC,再根据勾股定理求得AC=2![]() ,即可得到ABCD的面积=AB×AC=4×2
,即可得到ABCD的面积=AB×AC=4×2![]() =8
=8![]() .
.
解:(1)AC∥DE.理由:
由折叠可得,AB=AE,BC=EC,
又∵平行四边形ABCD中,AB=CD,BC=AD,
∴AE=CD,EC=DA,
又∵AC=CA,
∴△ACE≌△CAD,
∴∠ACE=∠CAD,
∴AF=CF,
∴EF=DF,
∴∠FED=∠FDE,
又∵∠DFE=∠AFC,
∴∠DEF=∠ACF,
∴AC∥DE;
(2)∵AF=CF,EF=DF,
∴当CE平分AD时,AF=DF=CF=EF,
∴四边形ACDE是矩形,
∴∠CAE=90°=∠BAC,
又∵AB=4,BC=6,
∴AC=![]() =2
=2![]() ,
,
∴ABCD的面积=AB×AC=4×2![]() =8
=8![]() .
.

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
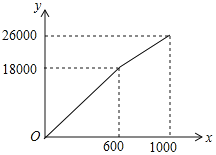
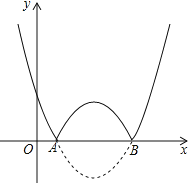
新黄冈兵法密卷系列答案【题目】为了创建“全国文明城市”,鄂州市积极主动建设美丽家园,某社区拟将一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草面积为x(m2),种草费用y1(元)与x(m2)的函数关系式为y1=![]() ,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
x(m2) | 100 | 200 | 300 |
y2(元) | 3900 | 7600 | 11100 |
(1)请直接写出y1与种草面积x(m2)的函数关系式,y2与栽花面积x(m2)的函数关系式;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与种草面积x(m2)的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于600m2,栽花部分的面积不少于200m2,请求出绿化总费用W的最小值.