题目内容
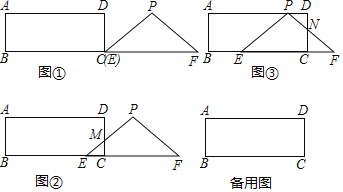
【题目】将两个全等的直角三角形ABC和DBE按图![]() 方式摆放,其中
方式摆放,其中![]() ,
,![]() ,点E落在AB上,DE所在直线交AC所在直线于点F.
,点E落在AB上,DE所在直线交AC所在直线于点F.
![]() 求证:
求证:![]() ;
;
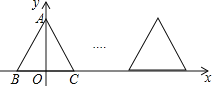
![]() 若将图
若将图![]() 中的
中的![]() 绕点B按顺时针方向旋转角a,且
绕点B按顺时针方向旋转角a,且![]() ,其他条件不变,如图
,其他条件不变,如图![]() 请你直接写出
请你直接写出![]() 与DE的大小关系:
与DE的大小关系:![]() ______
______![]() 填“
填“![]() ”或“
”或“![]() ”或“
”或“![]() ”
”![]()
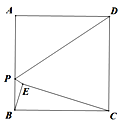
![]() 若将图
若将图![]() 中
中![]() 的绕点B按顺时针方向旋转角
的绕点B按顺时针方向旋转角![]() ,且
,且![]() ,其他条件不变,如图
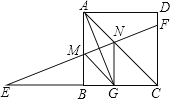
,其他条件不变,如图![]() 请你写出此时AF、EF与DE之间的关系,并加以证明.
请你写出此时AF、EF与DE之间的关系,并加以证明.

【答案】(1)证明见解析;(2)=;(3)AF-EF=DE.
【解析】
试题(1)如图,连接BF,由△ABC≌△DBE,可得BC=BE,根据直角三角形的“HL”定理,易证△BCF≌△BEF,即可证得;
(2)同(1)得CF=EF,由△ABC≌△DBE,可得AC=DE,AC=AF+CF=AF+EF,所以AF+EF=DE;
(3)同(1)得CF=EF,由△ABC≌△DBE,可得AC=DE,AF=AC+FC=DE+EF.
试题解析:
(1)证明:如图(1)连接BF, ∵Rt△ABC≌Rt△DBE,
∴BC=BE,
又BF=BF,
∴Rt△BCF≌Rt△BEF(HL),
∴CF![]() EF.
EF.
(2)=
(3)AF-EF=DE,
证明:如图(3),连接BF,
同(1)证明可知:CF![]() EF,
EF,
又DE![]() AC,
AC,
由图可知AF-CF=AC,
∴AF-EF=DE.
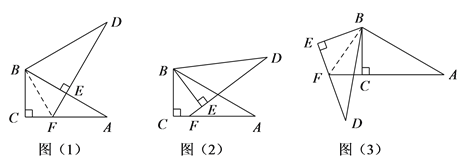

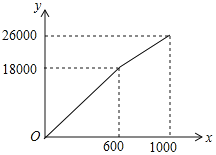
【题目】为了创建“全国文明城市”,鄂州市积极主动建设美丽家园,某社区拟将一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草面积为x(m2),种草费用y1(元)与x(m2)的函数关系式为y1=![]() ,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
x(m2) | 100 | 200 | 300 |
y2(元) | 3900 | 7600 | 11100 |
(1)请直接写出y1与种草面积x(m2)的函数关系式,y2与栽花面积x(m2)的函数关系式;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与种草面积x(m2)的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于600m2,栽花部分的面积不少于200m2,请求出绿化总费用W的最小值.