Question

【题目】如图，已知直线PA交⊙O于A、B两点，AE是⊙O的直径，点C为⊙O上一点，且AC平分∠PAE，过C作CD⊥PA，垂足为D．

（1）求证：CD为⊙O的切线；

（2）若DC+DA=6，⊙O的直径为10，求AB的长度．

Answer 1

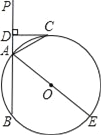
【答案】（1）证明见解析（2）6

【解析】分析:（1）连接OC，根据题意可证得∠CAD+∠DCA=90°，再根据角平分线的性质，得∠DCO=90°，则CD为 O的切线；

（2）过O作OF⊥AB，则∠OCD=∠CDA=∠OFD=90°，得四边形OCDF为矩形，设AD=x，在Rt△AOF中，由勾股定理得（5-x） +（6-x） =25，从而求得x的值，由勾股定理得出AB的长．

本题解析

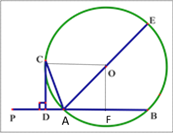
(1)证明：连接OC，∵OA=OC，∴∠OCA=∠OAC，∵AC平分∠PAE，

∴∠DAC=∠CAO，∴∠DAC=∠OCA，∴PB∥OC，∵CD⊥PA，

∴CD⊥OC，CO为O半径，∴CD为O的切线；

(2)过O作OF⊥AB，垂足为F，∴∠OCD=∠CDA=∠OFD=90，∴四边形DCOF为矩形，∴OC=FD，OF=CD.∵DC+DA=6，设AD=x，则OF=CD=6x，∵O的直径为10，∴DF=OC=5，∴AF=5x，

在Rt△AOF中,由勾股定理得AF +OF=OA.

即(5x) +(6x) =25，化简得x11x+18=0，

解得 .

∵CD=6x大于0，故x=9舍去，∴x=2，从而AD=2，AF=52=3，

∵OF⊥AB，由垂径定理知，F为AB的中点，∴AB=2AF=6.