题目内容
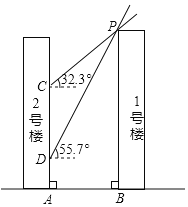
【题目】如图,1号楼在2号楼的南侧,楼间距为AB.冬至日正午,太阳光线与水平面所成的角为32.3°,1号楼在2号楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,1号楼在2号楼墙面上的影高为DA.已知CD=35m.请求出两楼之间的距离AB的长度(结果保留整数)
(参考数据:sin32.3°≈0.53,cos32.3°≈0.85,tan32.3°≈0.63,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
【答案】42m.
【解析】
构造出两个直角三角形,利用两个角的正切值即可求出答案.
解:过点C作CE⊥PB,垂足为E,过点D作DF⊥PB,垂足为F,
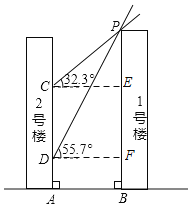
则∠CEP=∠PFD=90°,
由题意可知:设AB=x,
在Rt△PCE中,tan32.3°=![]() ,
,
∴PE=xtan32.3°,
同理可得:在Rt△PDF中,tan55.7°=![]() ,
,
∴PF=xtan55.7°,
由PF-PE=EF=CD=35,
可得xtan55.7°-xtan32.3°=35,
解得:x=42.
∴楼间距AB的长度约为42m.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目