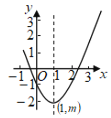题目内容
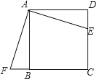
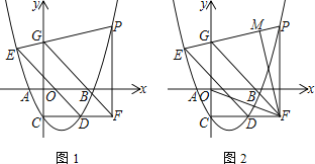
【题目】如图1,抛物线y=ax2-3ax-2交x轴于A、B(A左B右)两点,交y轴于点C,过C作CD∥x轴,交抛物线于点D,E(-2,3)在抛物线上.
(1)求抛物线的解析式;
(2)P为第一象限抛物线上一点,过点P作PF⊥CD,垂足为F,连接PE交y轴于G,求证:FG∥DE;
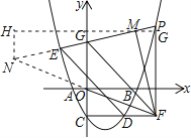
(3)如图2,在(2)的条件下,过点F作FM⊥PE于M.若∠OFM=45°,求P点坐标.
【答案】(1)y=![]() x2-
x2-![]() x-2;(2)见解析;(3)点P坐标为(6,7)
x-2;(2)见解析;(3)点P坐标为(6,7)
【解析】
(1)把点E坐标代入抛物线解析式即求得a的值;
(2)由抛物线解析式求点A、B、C、D的坐标,直接求得直线DE解析式为y=-x+1.设点P横坐标为t,即得到点F(t,-2).把t当常数用待定系数法求直线PE解析式,进而求得用t表示的点G纵坐标,再用待定系数法求直线FG解析式,解得FG解析式的一次项系数为-1,与直线DE相等,所以FG∥DE;
(3)延长FO、PE相交于点N,由FM⊥PE于M且∠OFM=45°可证得△MNF为等腰直角三角形,故有FM=MN.过点M作MG⊥PF于点G,过点N作NH⊥PM于点H,即构造出△FGM≌△MHN,进而有FG=MH,MG=NH.设点M横坐标为m,由(2)求得的直线PE解析式可得M的纵坐标,进而得到用t和m表示的MG、FG.求直线OF解析式,联立直线OF与直线PE求得用t表示的交点N坐标,进而得到用t和m表示的MH、NH.代入FG=MH,MG=NH即得到关于t、m的二元方程组,解方程组并考虑t的范围即求得点P坐标.
解:(1)∵E(-2,3)在抛物线y=ax2-3ax-2上
∴4a+6a-2=3
解得:a=![]()
∴抛物线解析式为y=![]() x2-
x2-![]() x-2
x-2
(2)证明:∵y=![]() x2-
x2-![]() x-2=0时,解得:x1=-1,x2=4
x-2=0时,解得:x1=-1,x2=4
∴A(-1,0),B(4,0)
∵x=0时,y=![]() x2-
x2-![]() x-2=-2
x-2=-2
∴C(0,-2)
∵点D在抛物线上,且CD∥x轴
∴D(3,-2)
设直线DE解析式为y=kx+b
∴![]() 解得:
解得:![]()
∴直线DE:y=-x+1
∵点P为第一象限抛物线上一点
∴设点P坐标为(t,![]() t2-
t2-![]() t-2)(t>4)
t-2)(t>4)
设直线PE解析式为y=cx+d
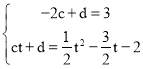 解得:
解得: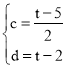
∴直线PE:y=![]() x+t-2,直线PE与y轴交点G(0,t-2)
x+t-2,直线PE与y轴交点G(0,t-2)
∵PF⊥CD于点F
∴F(t,-2)
设直线FG解析式为y=ex+t-2
把点F代入得:te+t-2=-2
解得:e=-1
∴FG∥DE
(3)延长FO、PE相交于点N,过点M作MG⊥PF于点G,过点N作NH⊥PM于点H
∴∠FGM=∠MHN=90°
∵FM⊥PE于M
∴∠FMN=90°
∴∠FMG+∠NMH=∠MNH+∠NMH=90°
∴∠FMG=∠MNH
∵∠OFM=45°
∴∠MNF=180°-∠FMN-∠OFM=45°
∴FM=MN
在△FGM与△MHN中
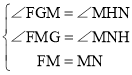
∴△FGM≌△MHN(AAS)
∴FG=MH,MG=NH
∵F(t,-2)
∴直线OF:y=-![]() x
x
∵点M在直线PE:y=![]() x+t-2上
x+t-2上
∴设M(m,![]() m+t-2)
m+t-2)
∴MG=t-m,FG=![]() m+t-2-(-2)=
m+t-2-(-2)=![]() m+t
m+t
∵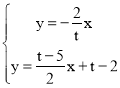 解得:
解得: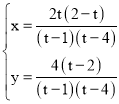
∴N(![]() ,
,![]() )
)
∴MH=m-![]() ,NH=
,NH=![]() m+t-2-
m+t-2-![]()
∴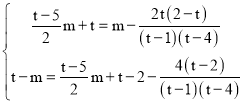
解得: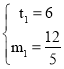
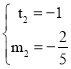 (舍去)
(舍去)
∴yP=![]() ×36-
×36-![]() ×6-2=7
×6-2=7
∴点P坐标为(6,7).