题目内容
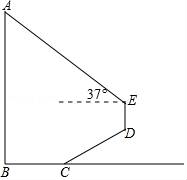
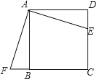
【题目】如图，正方形
中，
经顺时针旋转后与
重合．
旋转中心是点________，旋转了________度；
如果
，
，求：四边形
的面积．
【答案】（1）
,
；（2）详见解析.
【解析】
(1)根据正方形的性质得AB=AD,∠BAD=90
,则根据旋转的定义得到△ADE绕点A顺时针旋转90后与△ABF重合;
(2)根据旋转的性质得BF=DE,
=
,利用CF=CB+BF=8得到BC+DE=8,再加上
CE=CD-DE=BC-DE=4,于是可计算出BC=6,所以
=
=36.
解:(1)
四边形ABCD为正方形,
AB=AD,∠BAD=90,
△ADE绕点A顺时针旋转90后与△ABF重合,
即旋转中心是点A,旋转了90度;
故答案为A,90;
(2) △ADE绕点A顺时针旋转90后与△ABF重合,
BF=DE, =,
而CF=CB+BF=8,
BC+DE=8,
CE=CD-DE=BC-DE=4,
BC=6,
==6
=36
七星图书口算速算天天练系列答案
【题目】某公司计划从甲、乙两种产品中选择一种生产并销售，每年产销x件．已知产销两种产品的有关信息如下表：
产品 | 每件售价（万元） | 每件成本（万元） | 每年其他费用（万元） | 每年最大产销量（万元） |
甲 | 10 | a | 40 | 200 |
乙 | 18 | 8 | 40+0.05x2 | 100 |
其中a为常数，且5≤a≤8．
（1）若产销甲、乙两种产品的年利润分别为y1万元、y2万元，直接写出y1、y2与x的函数关系式；
（2）分别求出产销两种产品的最大年利润；
（3）为获得最大年利润，该公司应该选择产销哪种产品？请说明理由．
【题目】某工厂计划生产
，
两种产品共10件，其生产成本和利润如下表．
|
| |
成本(万元 | 2 | 5 |
利润(万元 | 1 | 3 |
（1）若工厂计划获利14万元，问，两种产品应分别生产多少件？
（2）若工厂计划投入资金不多于44万元，且获利多于22万元，问工厂有哪几种生产方案？
