题目内容
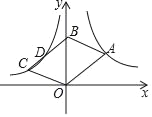
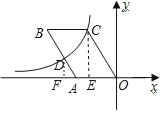
【题目】如图,ABCO的顶点B、C在第二象限,点A(﹣3,0),反比例函数y=![]() (k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )
(k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )

A. ﹣4tanαB. ﹣2sinαC. ﹣4cosαD. ﹣2tan
【答案】A
【解析】
过点C作CE⊥OA于E,过点D作DF⊥x轴于F,根据平行四边形的对边相等可得OC=AB,然后求出OC=2AD,再求出OE=2AF,设AF=a,表示出点C、D的坐标,然后根据CE、DF的关系列方程求出a的值,再求出OE、CE,然后利用∠COA的正切值列式整理即可得解.
如图,过点C作CE⊥OA于E,过点D作DF⊥x轴于F,
在OABC中,OC=AB,
∵D为边AB的中点,
∴OC=AB=2AD,CE=2DF,
∴OE=2AF,
设AF=a,∵点C、D都在反比例函数上,
∴点C(﹣2a,﹣![]() ),
),
∵A(3,0),
∴D(﹣a﹣3,![]() ),
),
∴-![]() =2×
=2×![]() ,
,
解得a=1,
∴OE=2,CE=﹣![]() ,
,
∵∠COA=∠α,
∴tan∠COA=tan∠α=![]() ,
,
即tanα=﹣![]() ,
,
k=﹣4tanα,
故选A.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目