Question

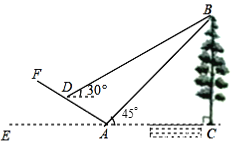
【题目】如图，小明为了测量小河对岸大树BC的高度，他在点A测得大树顶端B的仰角是45°，沿斜坡走米到达斜坡上点D，在此处测得树顶端点B的仰角为30°，且斜坡AF的坡比为1︰2．则小明从点A走到点D的过程中，他上升的高度为____米；大树BC的高度为____米（结果保留根号）．

Answer 1

【答案】 ；5+3.

【解析】

根据矩形性质得出DG=CH，CG=DH，再利用坡比及锐角三角函数的定义解直角三角形即可得答案．

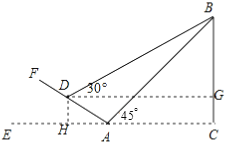
过点D作DG⊥BC于G，DH⊥CE于H，设上升的高度DH=x，

∴四边形DHCG是矩形，

∴DH=CG，DG=CH，

∵斜坡AF的坡比为1︰2，

∴AH=2DH=2x，

∴AH2+DH2=AD2，即(2x)2+x2=(2)2，

解得：x1=2，x2=-2(舍去)，

∴他上升的高度为2米.

∴AH=4，

∵∠BAC=45°，∠ACB=90°，

∴AC=BC，

在Rt△BDG中，

tan30°===，即：=，

解得：BC=5+3.

∴树BC高为5+3米.

故答案为：2；5+3