题目内容
【题目】如图,∠MAN=60°,AP平分∠MAN,点B是射线AP上一定点,点C在直线AN上运动,连接BC,将∠ABC(0°<∠ABC<120°)的两边射线BC和BA分别绕点B顺时针旋转120°,旋转后角的两边分别与射线AM交于点D和点E.

(1)如图1,当点C在射线AN上时,
①请判断线段BC与BD的数量关系,直接写出结论;
②请探究线段AC,AD和BE之间的数量关系,写出结论并证明;
(2)如图2,当点C在射线AN的反向延长线上时,BC交射线AM于点F,若AB=4,AC=![]() ,请直接写出线段AD和DF的长.
,请直接写出线段AD和DF的长.
【答案】(1)①BC=BD;②AD+AC=![]() BE;(2)AD=5
BE;(2)AD=5![]() , DF=
, DF=![]() .
.
【解析】试题分析:(1)①结论:BC=BD.只要证明△BGD≌△BHC即可.②结论:AD+AC=![]() BE.只要证明AD+AC=2AG=2EG,再证明EB=
BE.只要证明AD+AC=2AG=2EG,再证明EB=![]() BE即可解决问题;
BE即可解决问题;
(2)如图2中,作BG⊥AM于G,BH⊥AN于H,AK⊥CF于K.由(1)可知,△ABG≌△ABH,△BGD≌△BHC,易知BH,AH,BC,CH, AD的长,由sin∠ACH=![]() ,推出AK的长,设FG=y,则AF=
,推出AK的长,设FG=y,则AF=![]() ﹣y,BF=
﹣y,BF=![]() ,由△AFK∽△BFG,可得
,由△AFK∽△BFG,可得![]() ,可得关于y的方程,求出y即可解决问题.
,可得关于y的方程,求出y即可解决问题.
试题解析:(1)①结论:BC=BD,
理由:如图1中,作BG⊥AM于G,BH⊥AN于H,
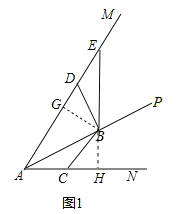
∵∠MAN=60°,PA平分∠MAN,BG⊥AM于G,BH⊥AN于H,∴BG=BH,∠GBH=∠CBD=120°,∴∠CBH=∠GBD,∵∠BGD=∠BHC=90°,∴△BGD≌△BHC,∴BD=BC;
②结论:AD+AC=![]() BE,
BE,
∵∠ABE=120°,∠BAE=30°,∴∠BEA=∠BAE=30°,∴BA=BE,∵BG⊥AE,∴AG=GE,EG=BEcos30°=![]() BE,∵△BGD≌△BHC,∴DG=CH,∵AB=AB,BG=BH,∴Rt△ABG≌Rt△ABH,∴AG=AH,∴AD+AC=AG+DG+AH﹣CH=2AG=
BE,∵△BGD≌△BHC,∴DG=CH,∵AB=AB,BG=BH,∴Rt△ABG≌Rt△ABH,∴AG=AH,∴AD+AC=AG+DG+AH﹣CH=2AG=![]() BE,∴AD+AC=
BE,∴AD+AC=![]() BE;
BE;
(2)如图2中,作BG⊥AM于G,BH⊥AN于H,AK⊥CF于K,
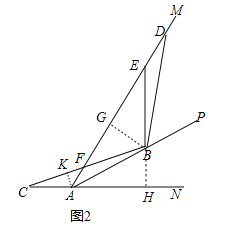
由(1)可知,△ABG≌△ABH,△BGD≌△BHC,
易知BH=GB=2,AH=AG=EG=![]() ,BC=BD=
,BC=BD=![]() =
=![]() ,CH=DG=
,CH=DG=![]() ,
,
∴AD=![]() ,∵sin∠ACH=
,∵sin∠ACH=![]() ,∴
,∴![]() ,∴AK=
,∴AK=![]() ,
,
设FG=y,则AF=![]() ﹣y,BF=
﹣y,BF=![]() ,
,
∵∠AFK=∠BFG,∠AKF=∠BGF=90°,
∴△AFK∽△BFG,∴![]() ,∴
,∴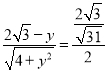 ,解得y=
,解得y=![]() 或
或![]() (舍弃),
(舍弃),
∴DF=GF+DG=![]() ,即DF=
,即DF=![]() .
.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案