题目内容
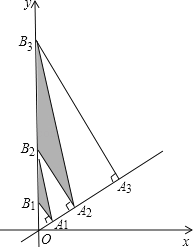
【题目】如图,直线y=![]() x上有点A1,A2,A3,…An+1,且OA1=1,A1A2=2,A2A3=4,AnAn+1=2n分别过点A1,A2,A3,…An+1作直线y=
x上有点A1,A2,A3,…An+1,且OA1=1,A1A2=2,A2A3=4,AnAn+1=2n分别过点A1,A2,A3,…An+1作直线y=![]() x的垂线,交y轴于点B1,B2,B3,…Bn+1,依次连接A1B2,A2B3,A3B4,…AnBn+1,得到△A1B1B2,△A2B2B3,△A3B3B4,…,△AnBnBn+1,则△AnBnBn+1的面积为________.(用含有正整数n的式子表示)
x的垂线,交y轴于点B1,B2,B3,…Bn+1,依次连接A1B2,A2B3,A3B4,…AnBn+1,得到△A1B1B2,△A2B2B3,△A3B3B4,…,△AnBnBn+1,则△AnBnBn+1的面积为________.(用含有正整数n的式子表示)
【答案】(22n﹣1﹣2n﹣1)![]()
【解析】∵直线OAn的解析式y=![]() x,∴∠AnOBn=60°.
x,∴∠AnOBn=60°.
∵OA1=1,A1A2=2,A2A3=4,AnAn+1=2n,∴A1B1=![]() ,A2B2=
,A2B2=![]() ,A3B3=
,A3B3=![]() .
.
设S=1+2+4+…+2n﹣1,则2S=2+4+8+…+2n,
∴S=2S﹣S=(2+4+8+…+2n)﹣(1+2+4+…+2n﹣1)=2n﹣1,
∴AnBn=(2n﹣1)![]() ,
,
∴![]() =
=![]() AnBnAnAn+1=
AnBnAnAn+1=![]() ×(2n﹣1)
×(2n﹣1)![]() ×2n=
×2n=![]() ,
,
故答案为: ![]() .
.

练习册系列答案
相关题目
【题目】根据下表回答下列问题:
x | 16.0 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 |
x2 | 256.00 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 |
(1)265.69的平方根是 , ![]() ;
;
(2)表中与![]() 最接近的数是 .
最接近的数是 .



