Question

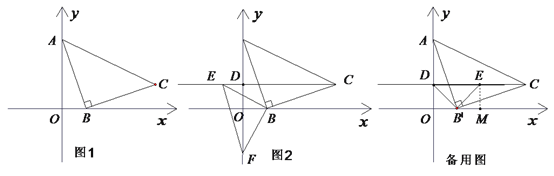
【题目】如图，在平面直角坐标系中，点 A，B的坐标分别为（0，3），（1，0），△ABC是等腰直角三角形，∠ABC＝90°．

（1）图1中，点C的坐标为 ；

(2)如图2，点D的坐标为（0，1），点E在射线CD上，过点B 作BF⊥BE交y轴于点F．

①当点E为线段CD的中点时，求点F的坐标；

②当点E在第二象限时，请直接写出F点纵坐标y的取值范围．

Answer 1

【答案】(1 ) C(4，1)；（2）①F( 0 , 1 )，②

【解析】试题分析： 过点向轴作垂线，通过三角形全等，即可求出点坐标.

过点E作EM⊥x轴于点M，根据的坐标求出点的坐标，OM=2，得到 得到△OBF为等腰直角三角形，即可求出点的坐标.

直接写出点纵坐标的取值范围．

试题解析：(1 ) C(4，1)，

（2）法一：过点E作EM⊥x轴于点M，

∵C（4，1），D（0，1），E为CD中点，

∴CD∥x轴，EM=OD=1，

∴OM=2，

∴∠OBF=45°，

∴ △OBF为等腰直角三角形，

∴OF=OB=1.

法二：在OB的延长线上取一点M.

∵∠ABC=∠AOB=90°.

∴∠ABO+∠CBM=90° .

∠ABO+∠BAO =90°.

∴∠BAO=∠CBM .

∵C(4,1).

D(0,1).

又∵CD∥OM ,CD=4.

∴∠DCB=∠CBM.

∴∠BAO=∠ECB.

∵∠ABC=∠FBE=90°.

∴∠ABF=∠CBE.

∵AB=BC.

∴△ABF≌△CBE(ASA).

∴AF=CE=CD=2,

∵A(0,3),

OA=3,

∴OF=1.

∴F(0,1) ,

(3) .