题目内容
【题目】如图,已知二次函数y=ax2+bx+c的象经过A(﹣1,0)、B(3,0)、N(2,3)三点,且与y轴交于点C.
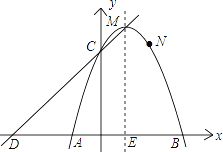
(1)求这个二次函数的解析式,并写出顶点M及点C的坐标;
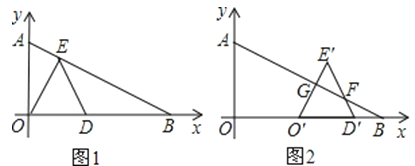
(2)若直线y=kx+d经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;
(3)点P是这个二次函数的对称轴上一动点,请探索:是否存在这样的点P,使以点P为圆心的圆经过A、B两点,并且与直线CD相切?如果存在,请求出点P的坐标;如果不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3,顶点M(1,4),点C(0,3);(2)见解析;
(3)点P存在,其坐标为(1,![]() )或(1,
)或(1,![]() ) .
) .
【解析】
(1)将点A、B、C的坐标代入y=ax2+bx+c中建立方程组,解方程组求得a、b、c的值即可得到所求的解析式,再由所得解析式求出顶点M的坐标和点C的坐标即可;
(2)根据(1)中所得点M、C的坐标求得直线CM的解析式,即可求得点D的坐标,然后结合已知条件证得CD=AN,AD=CN,即可证得四边形CDAN是平行四边形;
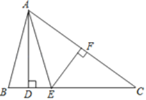
(3)如下图,若圆P过A、B两点,设点P的坐标为(1,y0),过点P作PQ⊥CM于点M,则当PQ=PA时,圆P和直线CM相切,由此结合已知条件列出关于y0的方程,解方程求出y0的值即可得到所求的点P的坐标.
(1)∵二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、B(3,0)、N(2,3)
∴可建立方程组: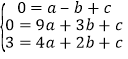 ,解得:
,解得: 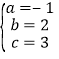 ,
,
∴所求二次函数的解析式为y=﹣x2+2x+3,
∵y=-(x-1)2+4,
∴顶点M的坐标为:(1,4),
∵在y=-x2+2x+3中,当x=0时,y=3,
∴点C的坐标为:(0,3)
(2)∵直线y=kx+d经过C、M两点,
∴ ![]() ,解得:即k=1,d=3,
,解得:即k=1,d=3,
∴直线CM的解析式为y=x+3.
∵在y=x+3中,当y=0时,x=﹣3,
∴点D的坐标为:(﹣3,0),
∵点C、A、N的坐标分别为(0,3)、(-1,0)、(2,3),
∴CD= ![]() ,AN=
,AN=![]() ,AD=2,CN=2,
,AD=2,CN=2,
∴CD=AN,AD=CN,
∴四边形CDAN是平行四边形;
(3)假设存在这样的点P,使以点P为圆心的圆经过A、B两点,并且与直线CD相切,
∵二次函数y=-(x-1)2+4的对称轴是直线x=1,
∴可设P的坐标为:(1,y0),
∴PA是圆P的半径且PA2=y02+22 ,
如下图,过点P做PQ⊥CD于Q,则当PQ=PA时,以P为圆心的圆与直线CD相切.
∵D、M、E的坐标分别为(-3,0)、(1,4)、(1,0),
∴DE=ME=4,ME⊥DE,
∴△MDE为等腰直角三角形,
∴△PQM也是等腰直角三角形,
由点P的坐标为(1,y0)可得PE=y0 ,
∴PM=|4﹣y0|,
∴![]() ,
,
由PQ2=PA2时,圆P和直线CM相切,可得方程:
![]() ,
,
解得![]() ,
,
∴满足题意的点P存在,其坐标为(1,![]() )或(1,
)或(1,![]() ) .
) .


 名校课堂系列答案
名校课堂系列答案【题目】已知甲、乙两袋中各装有若干颗球,其种类与数量如表所示.今阿冯打算从甲袋中抽出一颗球,小潘打算从乙袋中抽出一颗球,若甲袋中每颗球被抽出的机会相等,且乙袋中每颗球被抽出的机会相等,则下列叙述何者正确?( )
甲袋 | 乙袋 | |
红球 | 2颗 | 4颗 |
黄球 | 2颗 | 2颗 |
绿球 | 1颗 | 4颗 |
总计 | 5颗 | 10颗 |
A. 阿冯抽出红球的机率比小潘抽出红球的机率大
B. 阿冯抽出红球的机率比小潘抽出红球的机率小
C. 阿冯抽出黄球的机率比小潘抽出黄球的机率大
D. 阿冯抽出黄球的机率比小潘抽出黄球的机率小