题目内容
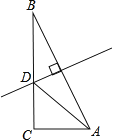
【题目】CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由.
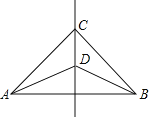
解:∵CD是线段AB的垂直平分线(已知),
∴AC=______,______=BD(______)
在△ADC和______中,
______=BC,
AD=______,
CD=______(______),
∴______≌______(______ ).
∴∠CAD=∠CBD (全等三角形的对应角相等).
【答案】BC AD 线段垂直平分线上的点到线段两端的距离相等 △BDC AC BD CD 公共边 △ADC △BDC SSS
【解析】
利用垂直平分线的性质,可以得到2个等腰三角形,△ACB和△ADB,再根据全等的判定,可以证得△ADC≌△BDC.
∵CD是线段AB的垂直平分线(已知),
∴AC=BC,AD=BD(线段垂直平分线上的点到线段两个端点的距离相等),
在△CBD和△CAD中
AC=BC
AD=BD
CD=CD
∴△CBD≌△CAD(SSS),
∴∠CAD=∠CBD(全等三角形的对应角相等),

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目