题目内容
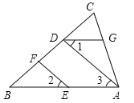
【题目】在Rt△ABO中,∠AOB=90°,OA=![]() ,OB=4,分别以OA、OB边所在的直线建立平面直角坐标系,D为x轴正半轴上一点,以OD为一边在第一象限内作等边△ODE.
,OB=4,分别以OA、OB边所在的直线建立平面直角坐标系,D为x轴正半轴上一点,以OD为一边在第一象限内作等边△ODE.
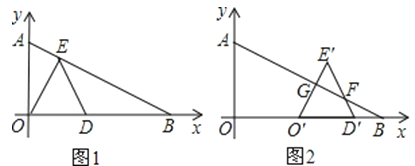
(1)如图①,当E点恰好落在线段AB上时,求E点坐标;
(2)在(Ⅰ)问的条件下,将△ODE沿x轴的正半轴向右平移得到△O′D′E′,O′E′、D′E′分别交AB于点G、F(如图②)求证OO′=E′F;
(3)若点D沿x轴正半轴向右移动,设点D到原点的距离为x,△ODE与△AOB重叠部分的面积为y,请直接写出y与x的函数关系式.
【答案】(1)E(1,![]() );(2)证明见解析;(3)见解析.
);(2)证明见解析;(3)见解析.
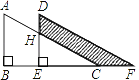
【解析】(1)由题意作辅助线,作EH⊥OB于点H,由BO=4,求得OE,然后求出OH,EH,从而得出点E的坐标;
(2)假设存在,由OO′=4-2-DB,而DF=DB,从而得到OO′=EF;
(3)根据题意分三种情况写出解析式即可.
(1)作EH⊥OB于点H,
tan∠ABO=![]() =
=![]() =
=![]() ,
,
∴∠ABO=30°,
∵△OED是等边三角形,
∴∠EOD=60°.
又∵∠ABO=30°,
∴∠OEB=90°.
∵BO=4,
∴OE=![]() OB=2.
OB=2.
∵△OEH是直角三角形,且∠OEH=30°
∴OH=1,EH=![]() .
.
∴E(1,![]() );
);
(2)∵∠ABO=30°,∠EDO=60°,
∴∠ABO=∠DFB=30°,
∴D′F=D′B.
∴OO′=4﹣2﹣D′B=2﹣D′B=2﹣D′F=E′D′﹣FD′=E′F;
(3)当0<x≤2时,△ODE与△AOB重叠部分的面积为△ODE面积=![]() x2,
x2,
当2<x<4时,△ODE与△AOB重叠部分的面积为四边形GO′DF面积=﹣![]() x2+2
x2+2![]() x﹣2
x﹣2![]() ,
,
当x≥4时,△ODE与△AOB重叠部分的面积为2![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目